
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 14 gợi ý nè:
a) Gọi d là ƯCLN(4n+1;5n+1)
Sử dụng tính chất chia hết của 1 hiệu, ta phải có 4n+1 và 5n+1 chia hết cho d
Lấy số lớn trừ số bé, ta có : (5n+1)-(4n+1) chia hết cho d => chỉ còn 1 chia hết cho d => d=1
Vậy ƯCLN(4n+1;5n+1)=1
Câu b giải tương tự như trên bạn nhé



A = 10,11 + 11,12 + 12,13 + . . .+ 98,99 + 99,10
Ta có :
10,11 = 10 + 0,11
11,12 = 11 + 0,12
12,13 = 12 + 0,13
. . . . . . . . . . . . . .
97,98 = 97 + 0,98
98,99 = 98 + 0,99
99,10 = 99 + 0,10
Đặt B = 10 + 11 + 12 + 13 + . .. +98 + 99
và C = 0,11 + 0,12 + 0,13 + . . . .+ 0,98 + 0,99 + 0,10
- - > 100C = 11 + 12 + 13 + . . .+ 98 + 99 + 10
Ta chỉ việc tính B là suy ra C !
B = 10 + 11 + 12 + 13 + . .. +98 + 99
B = (10+99)+(11+98)+(12+97)+. . . +(44+65) + (45 + 64)
Vì từ 10 đến 99 có tất cả 90 số . Ta sẽ có 90/2 = 45 cặp
Mỗi cặp có tổng là 10 + 99 = 11 + 98 = . .= 45 +64 = 109
Vậy ta có B = 45.109 = 4905
Với A = 4905 . Ta thấy 100C = 10 + 11 + 12 +. . + 98 + 99 =B
- - > 100C = 4905 . Hay C = 4905/100 = 49,05
Vậy A = B + C = 4905 + 49,05 = 4954,05

Từ đề bài ta có:
\(T=\dfrac{1+2}{2}.\dfrac{1+3}{3}.\dfrac{1+4}{4}...\dfrac{1+98}{98}.\dfrac{1+99}{99}\)
\(=\dfrac{3}{2}.\dfrac{4}{3}.\dfrac{5}{4}...\dfrac{99}{98}.\dfrac{100}{99}\)
\(=\dfrac{100}{2}\)
\(=50\).
\(T=\left(\dfrac{1}{2}+1\right)\left(\dfrac{1}{3}+1\right)\left(\dfrac{1}{4}+1\right)...\left(\dfrac{1}{98}+1\right)\left(\dfrac{1}{99}+1\right)\)
\(T=\dfrac{3}{2}.\dfrac{4}{3}.\dfrac{5}{4}....\dfrac{99}{98}.\dfrac{100}{99}\)
\(T=\dfrac{3.4.5......99}{3.4.5......99}.\dfrac{100}{2}\)
\(T=50\)

Theo mk được biết thì Shinichi và Kid là hai anh em nên mk thích cả hai
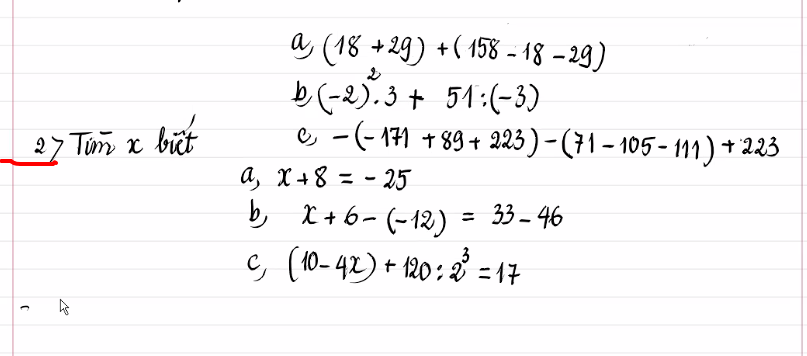



 àm vòng tròn
àm vòng tròn




 giải giùm tớ nha
giải giùm tớ nha

Bài 1 :
a) \(\left(18+29\right)+\left(158-18-29\right)\)
\(=\left(18-18\right)+\left(29-29\right)+158\)
\(=0+0+158\)
\(=0+158\)
\(=158\)
b) \(\left(-2\right)^2.3+51:\left(-3\right)\)
\(=4.3+-17\)
\(=12+-17\)
\(=-34\)
làm tiếp cho mình nhé?