Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

4.
Đáp án A đúng
\(y'=9x^2+3>0;\forall v\in R\)
6.
Đáp án B đúng
\(y'=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(\Rightarrow\) Hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Do \(\left(2;+\infty\right)\subset\left(1;+\infty\right)\) nên hàm cũng đồng biến trên \(\left(2;+\infty\right)\)

bạn chỉ cần tách x4-1 thành (x2-1)(x2+1),rồi đặt x2=t là ok


bạn tải về rồi zoom lên ý, vì đây là tớ chụp ảnh nên ảnh nhỏ
mong bạn tải về zoom lên hướng dẫn tớ với

Lời giải:
Đặt \(2^{x^2}=t\). Khi đó \(t\geq 1\)
PT trở thành: \(t^2-4t+6=m\Leftrightarrow t^2-4t+(6-m)=0\) (*)
Tư duy:
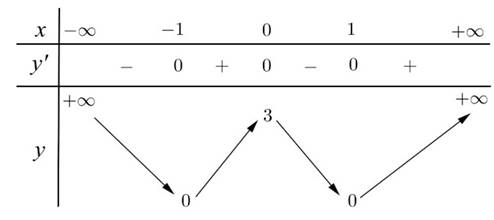
Nếu (*) có 1 nghiệm duy nhất thì $x^2$ là duy nhất, do đó pt ban đầu chỉ có thể có nhiều nhất 2 nghiệm
Nếu (*) có 2 nghiệm đều khác 1, khi đó $x^2$ có hai giá trị đều khác $0$, kéo theo pt ban đầu có 4 nghiệm
Như vậy, để PT ban đâu có 3 nghiệm thì (*) phải có 2 nghiệm phân biệt , trong đó một nghiệm bằng $1$. Bởi vì khi đó, nghiệm $t$ khác 1 sẽ cho 2 giá trị của $x$, nghiệm $t=1$ cho giá trị $x=0$ duy nhất.
Vậy (*) có nghiệm là $1$, tức là
\(1^2-4.1+(6-m)=0\Leftrightarrow 3-m=0\Leftrightarrow m=3\)
Thử lại thấy thỏa mãn
Đáp án D

Đặt MA=x \(\Rightarrow\)MB= 24-x với \(x\in\left[0;24\right]\)
Đặt f(x)=MC+MD=\(\sqrt{MA^2+AC^2}+\sqrt{MB^2+BD^2}=\sqrt{x^2+10^2}+\sqrt{\left(24-x^2\right)+30^2}\)
Ta xét hàm f(x) trên đoạn [0;24]
\(f'\left(x\right)=\frac{x}{\sqrt{x^2+10^2}}-\frac{24-x}{\sqrt{\left(24-x\right)^2+30^2}}\\ =\frac{MA}{MC}-\frac{MB}{MD}\)
\(f'\left(x\right)=0\Leftrightarrow\frac{MA}{MC}-\frac{MB}{MD}=0\Leftrightarrow\frac{MA}{MC}=\frac{MB}{MD}\)
từ đó suy ra hai tam giác vuông \(\Delta MAC\) và \(\Delta MBD\) đồng dạng
\(\Rightarrow\frac{MA}{MC}=\frac{MB}{MD}=\frac{AC}{BD}=\frac{1}{3}\)
Vậy \(MA=\frac{24}{3+1}=6\)(m) và MB=24-6=18(m)

gọi a,b,c(cm) lần lượt là số đo 3 chiều của hình hộp
Ta có: \(S_1=a.b\\ S_2=b.c\\ S_3=a.c\)
\(\Rightarrow V=a.b.c=\sqrt{S_1.S_2.S_3}=\sqrt{20.28.35}=140\left(cm^3\right)\)












Gọi \(A_1\) là biến cố: "quả cầu lấy ra thuộc thùng I"
\(A_2\) là biến cố: "quả cầu lấy ra thuộc thùng II"
\(A_3\) là biến cố: "quả cầu lấy ra thuộc thùng III"
\(\Rightarrow A_1;A_2;A_3\) là nhóm biến cố đầy đủ
Gọi B là biến cố: "quả cầu lấy ra là cầu trắng".
\(\Rightarrow P\left(B|A_1\right)=\dfrac{6}{10}=\dfrac{3}{5};P\left(B|A_2\right)=\dfrac{5}{11};P\left(B|A_3\right)=\dfrac{1}{4}\)
Khi lấy ngẫu nhiên 1 thùng từ 3 thùng, xác suất được chọn của 3 thùng bằng nhau: \(P\left(A_1\right)=P\left(A_2\right)=P\left(A_3\right)=\dfrac{1}{3}\)
\(\Rightarrow P\left(B\right)=P\left(B|A_1\right).P\left(A_1\right)+P\left(B|A_2\right).P\left(A_2\right)+P\left(B|A_3\right).P\left(A_3\right)\)
\(=\dfrac{3}{5}.\dfrac{1}{3}+\dfrac{5}{11}.\dfrac{1}{3}+\dfrac{1}{4}.\dfrac{1}{3}=\dfrac{287}{660}\)
a.
\(P\left(A_2|B\right)=\dfrac{P\left(A_2\right).P\left(B|A_2\right)}{P\left(B\right)}=\dfrac{100}{287}\)
b.
\(P\left(A_1|B\right)=\dfrac{P\left(A_1\right).P\left(B|A_1\right)}{P\left(B\right)}=\dfrac{132}{287}\)
Do \(P\left(A_1|B\right)>P\left(A_2|B\right)\) nên xác suất nó thuộc thùng I cao hơn