Giúp mình gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 4 2022
a.
\(0< a< \dfrac{\pi}{2}\Rightarrow cosa>0\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{4}{5}\)
\(\Rightarrow tana=\dfrac{sina}{cosa}=\dfrac{3}{4}\) ; \(cota=\dfrac{1}{tana}=\dfrac{4}{3}\)
\(\Rightarrow A=\dfrac{\dfrac{4}{3}+\dfrac{3}{4}}{\dfrac{4}{3}-\dfrac{3}{4}}=...\)
b.
\(A=\dfrac{\dfrac{2sina}{cosa}+\dfrac{3cosa}{cosa}}{\dfrac{4sina}{cosa}-\dfrac{5cosa}{cosa}}=\dfrac{2tana+3}{4tana-5}=\dfrac{2.3+3}{4.3-5}=...\)
\(B=\dfrac{\dfrac{3sina}{cos^3a}-\dfrac{2cosa}{cos^3a}}{\dfrac{5sin^3a}{cos^3a}+\dfrac{4cos^3a}{cos^3a}}=\dfrac{3tana\left(1+tan^2a\right)-2\left(1+tan^2a\right)}{5tan^3a+4}=...\) em tự thay số
c.
\(B=\dfrac{cos^2x+2sinx.cosx+1}{sin^2x+3}=\dfrac{\dfrac{cos^2x}{cos^2x}+\dfrac{2sinx.cosx}{cos^2x}+\dfrac{1}{cos^2x}}{\dfrac{sin^2x}{cos^2x}+\dfrac{3}{cos^2x}}\)
\(=\dfrac{1+2tanx+\left(1+tan^2x\right)}{tan^2x+3\left(1+tan^2x\right)}=...\)
10 tháng 9 2023
a: A={0;1;2;3;4;5}
b: B={-2;-1;0;1;2;3}
c: C={2;-2}
d: D={-3;-2;-1;0;1;2;3}
e: E={0;1;-1;2;-2}
f: 8-x^2>2
=>-x^2>-6
=>x^2<6
=>-căn 6<x<căn 6
mà x thuộc N
nên \(x\in\left\{0;1;2\right\}\)
=>F={0;1;2}
g: G={-10;-5;0;5;10;15}
h: H={-2;1}
i: x<10
=>m^2-3<10
=>m^2<13
=>\(-\sqrt{13}< m< \sqrt{13}\)
mà m thuộc N
nên \(m\in\left\{0;1;2;3\right\}\)
=>I={-3;-2;1;6}
j: 2^n-5<0
=>2^n<5
mà n thuộc N
nên \(n\in\left\{0;1;2\right\}\)
=>J={-4;-3;-1}
30 tháng 12 2021
1: \(\overrightarrow{AB}=\left(-3;-1\right)\)
\(\overrightarrow{AC}=\left(1;2\right)\)
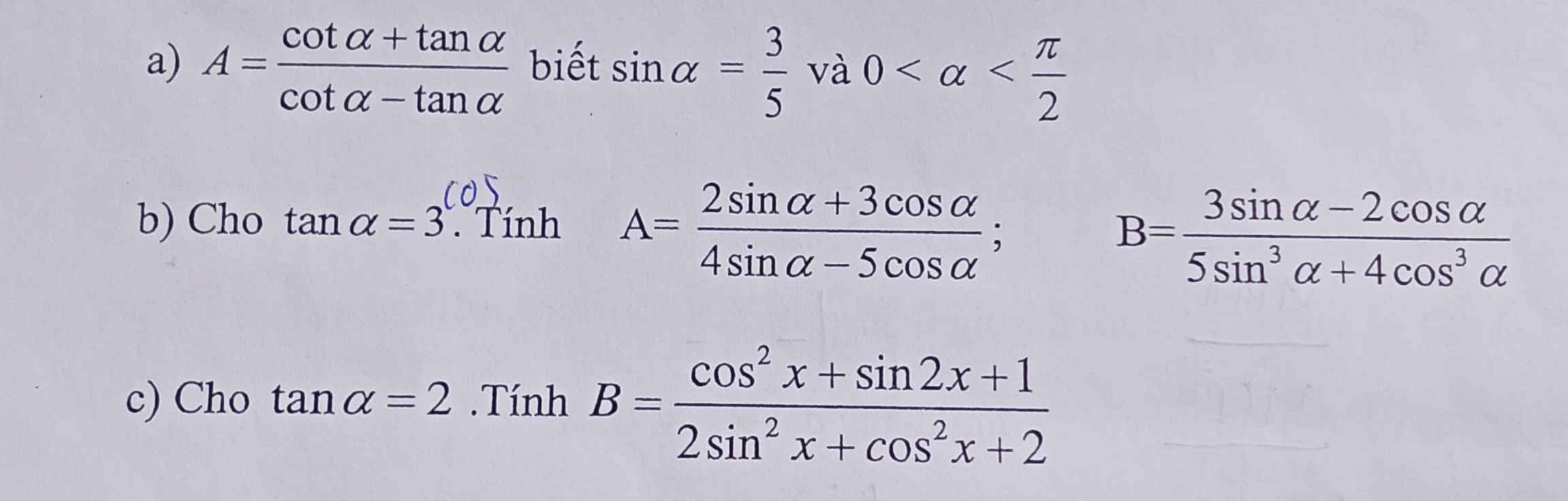
B. \(A=sin\left(a+b\right)+sin\left(\frac{\pi}{2}-a\right)sin\left(-b\right)\)
\(=sina.cosb+cosa.sinb+cosa.\left(-sinb\right)\)
\(=sina.cosb\).