
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét phương trình tiếp tuyến tổng quát có dạng:
\(y=\left(6x_0+3x_0^2\right)\left(x-x_0\right)+3x_0^2+x_0^3\)
có 3 tiếp tuyến đi qua A(a,0) nên phương trình \(\left(6x_0+3x_0^2\right)\left(a-x_0\right)+3x_0^2+x_0^3=0\) có 3 nghiệm
\(PT\Leftrightarrow\orbr{\begin{cases}x_0=0\\2x_0^2+3\left(1-a\right)x_0+6a=0\end{cases}}\)
Vậy có 1 pttt là y=0
do đó để có hai tiếp tuyến vuông góc thì \(2x_0^2+3\left(1-a\right)x_0+6a=0\) có hia nghiệm \(x_1,x_2\text{ thỏa mãn}\)
\(\left(6x_1+3x_1^2\right)\left(6x_2+3x_2^2\right)=-1\)mà áp dung Viet ta có \(\hept{\begin{cases}x_1+x_2=\frac{3a-3}{2}\\x_1x_2=3a\end{cases}}\)
Nên \(36x_1x_2+18x_1x_2\left(x_1+x_2\right)+9x_1^2x_2^2=-1\Leftrightarrow126a+81a\left(a-1\right)+81a^2=-1\)
từ đây mình giải được a nhé
Xét phương trình tiếp tuyến tổng quát có dạng:
y=(6x0+3x02)(x−x0)+3x02+x03
có 3 tiếp tuyến đi qua A(a,0) nên phương trình (6x0+3x02)(a−x0)+3x02+x03=0 có 3 nghiệm
PT⇔[
| x0=0 |
| 2x02+3(1−a)x0+6a=0 |
Vậy có 1 pttt là y=0
do đó để có hai tiếp tuyến vuông góc thì 2x02+3(1−a)x0+6a=0 có hia nghiệm x1,x2 thỏa mãn
(6x1+3x12)(6x2+3x22)=−1mà áp dung Viet ta có {
| x1+x2=3a−32 |
| x1x2=3a |
Nên 36x1x2+18x1x2(x1+x2)+9x12x22=−1⇔126a+81a(a−1)+81a2=−1

a)tan (2x+1)*tan (3x-1)=1
\(\Rightarrow\frac{sin\left(2x+1\right)}{cos\left(2x+1\right)}\cdot\frac{sin\left(3x-1\right)}{cos\left(2x-1\right)}=1\)
\(\Rightarrow cos5xcos\left(2-x\right)-cos5x=cos5x+cos\left(2-x\right)\)
\(\Rightarrow2cos5x=0\)
\(\Rightarrow x=\frac{\pi}{10}+\frac{k\pi}{5}\)
b)Đk:\(cosx\ne0,cos\left(x+\frac{\pi}{4}\right)\)
\(pt\Leftrightarrow tanx+\frac{1+tanx}{1-tanx}=1\)
\(\Leftrightarrow tanx\left(1-tanx\right)+1+tanx=1-tanx\)
\(\Leftrightarrow tanx\cdot\left(1-tanx\right)+2tanx=0\)
\(\Leftrightarrow tanx\left(1-tanx+2\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}tanx=0\\tanx=3\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=k\pi\\x=a+k\pi\left(a=arctan3\right)\end{array}\right.\)


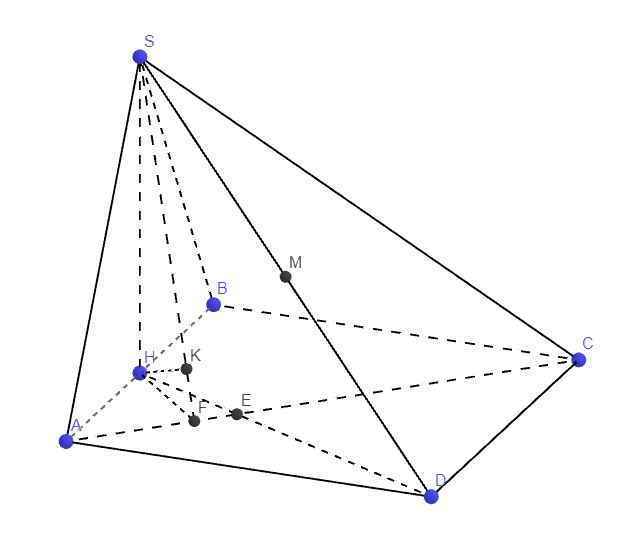
Gọi H là trung điểm AB, có lẽ từ 2 câu trên ta đã phải chứng minh được \(SH\perp\left(ABCD\right)\)
Do \(\left\{{}\begin{matrix}DM\cap\left(SAC\right)=S\\MS=\dfrac{1}{2}DS\end{matrix}\right.\) \(\Rightarrow d\left(M;\left(SAC\right)\right)=\dfrac{1}{2}d\left(D;\left(SAC\right)\right)\)
Gọi E là giao điểm AC và DH
Talet: \(\dfrac{HE}{DE}=\dfrac{AH}{DC}=\dfrac{1}{2}\Rightarrow HE=\dfrac{1}{2}DE\)
\(\left\{{}\begin{matrix}DH\cap\left(SAC\right)=E\\HE=\dfrac{1}{2}DE\end{matrix}\right.\) \(\Rightarrow D\left(H;\left(SAC\right)\right)=\dfrac{1}{2}d\left(D;\left(SAC\right)\right)=d\left(M;\left(SAC\right)\right)\)
Từ H kẻ HF vuông góc AC (F thuộc AC), từ H kẻ \(HK\perp SF\)
\(\Rightarrow HK\perp\left(SAC\right)\Rightarrow HK=d\left(H;\left(SAC\right)\right)\)
ABCD là hình vuông \(\Rightarrow\widehat{HAF}=45^0\Rightarrow HF=AH.sin45^0=\dfrac{a\sqrt{2}}{4}\)
\(SH=\dfrac{a\sqrt{3}}{2}\), hệ thức lượng:
\(HK=\dfrac{SH.HF}{\sqrt{SH^2+HF^2}}=\dfrac{a\sqrt{21}}{14}\)
\(\Rightarrow d\left(M;\left(SAC\right)\right)=\dfrac{a\sqrt{21}}{14}\)



ĐKXĐ: \(-2\le x\le3\)
Đặt \(\sqrt{x+2}+2\sqrt{3-x}=a\Rightarrow4\sqrt{6+x-x^2}-3x=a^2-14\)
Mặt khác \(a^2=\left(\sqrt{x+2}+2\sqrt{3-x}\right)^2\le5\left(x+2+3-x\right)=25\)
\(\Rightarrow a\le5\)
Và \(\sqrt{x+2}+\sqrt{3-x}+\sqrt{3-x}\ge\sqrt{5}+\sqrt{3-x}\ge\sqrt{5}\) \(\Rightarrow a\ge\sqrt{5}\)
\(\Rightarrow\sqrt{5}\le a\le5\)
Phương trình trở thành:
\(a^2-14=ma\Leftrightarrow\frac{a^2-14}{a}=m\) với \(a\in\left[\sqrt{5};5\right]\)
\(f\left(a\right)=\frac{a^2-14}{a}\Rightarrow f'\left(a\right)=\frac{2a^2-a^2+14}{a^2}=\frac{a^2+14}{a^2}>0\)
\(\Rightarrow f\left(a\right)\) đồng biến \(\Rightarrow f\left(\sqrt{5}\right)\le f\left(a\right)\le5\)
\(\Rightarrow-\frac{9\sqrt{5}}{5}\le f\left(a\right)\le\frac{11}{5}\Rightarrow-\frac{9\sqrt{5}}{5}\le m\le\frac{11}{5}\)

Câu 1: \(\frac{\pi}{2}<\alpha,\beta<\pi\)
=>\(\sin\alpha>0;\sin\beta>0;cos\alpha<0;cos\beta<0\)
\(\sin^2\alpha+cos^2\alpha=1\)
=>\(cos^2\alpha=1-\sin^2\alpha=1-\left(\frac13\right)^2=\frac89\)
mà \(cos\alpha<0\)
nên \(cos\alpha=-\frac{2\sqrt2}{3}\)
Ta có: \(\sin^2\beta+cos^2\beta=1\)
=>\(\sin^2\beta=1-\left(-\frac23\right)^2=1-\frac49=\frac59\)
mà \(\sin\beta>0\)
nên \(\sin\beta=\frac{\sqrt5}{3}\)
\(\sin\left(\alpha+\beta\right)=\sin\alpha\cdot cos\beta+cos\alpha\cdot\sin\beta\)
\(=\frac13\cdot\frac{-2}{3}+\frac{-2\sqrt2}{3}\cdot\frac{\sqrt5}{3}=\frac{-\sqrt2-2\sqrt{10}}{9}\)
Câu 2:
\(P=cos\left(a+b\right)\cdot cos\left(a-b\right)\)
\(=\frac12\cdot\left\lbrack cos\left(a+b+a-b\right)+cos\left(a+b-a+b\right)\right\rbrack=\frac12\cdot\left\lbrack cos2a+cos2b\right\rbrack\)
\(=\frac12\cdot\left\lbrack2\cdot cos^2a-1+2\cdot cos^2b-1\right\rbrack=cos^2a+cos^2b-1\)
\(=\left(\frac13\right)^2+\left(\frac14\right)^2-1=\frac19+\frac{1}{16}-1=\frac{25}{144}-1=-\frac{119}{144}\)



 giúp mình với ạ
giúp mình với ạ đây là phương trình tổ hợp ,mọi người giúp mình với, mình phải kiểm tra gấp
đây là phương trình tổ hợp ,mọi người giúp mình với, mình phải kiểm tra gấp




 giúp t với ạ
giúp t với ạ
