Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) HS tự tìm
b) Sử dụng các cặp góc so le trong của hai đường thẳng song song và tính chất tia phân giác.
c) Suy ra từ b)

em tự vẽ hình
câu 1 em tự chứng minh nhé
câu 2,
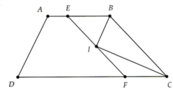
ta có IE//BC\(\Rightarrow\widehat{EIC}=\widehat{ICB}\) (so le trong)
mà \(\widehat{ECI}=\widehat{ICB}\) (phân giác )
=> \(\widehat{EIC}=\widehat{ECI}\)
=> tam giác IEC cân tại E
chứng minh tương tự cvới tam giác kia nhé
c)
ta có tam giác IEC cân tại E=> IE=EC
vơi tam giác kia cân thì ta có IF=FB
=> IE+IF=BF+CE
=> EF=BF+IC

Bài 2:
a: Xét ΔABE và ΔACF có
góc ABE=góc ACF
AB=AC
góc A chung
Do đó: ΔABE=ΔACF
Suy ra: AE=AF
b: Xét ΔABC có AF/AB=AE/AC
nên FE//BC
=>BFEC là hình thang
mà CF=BE
nên BFEC là hình thang cân
c: Xét ΔFEB có góc FEB=góc FBE
nên ΔFEB cân tại F
=>FE=FB=EC

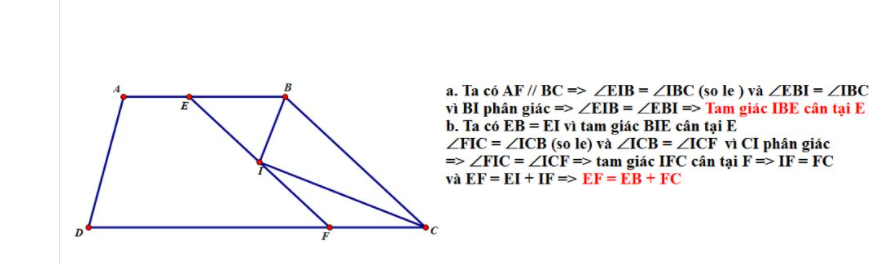
\(a,\) Ta có \(\widehat{B_1}=\widehat{B_2}\left(t/c.phân.giác\right);\widehat{B_2}=\widehat{I_1}\left(so.le.trong.do.EI//BC\right)\)
\(\Rightarrow\widehat{B_1}=\widehat{I_1}\Rightarrow\Delta BEI.cân.tại.E\)
Ta có \(\widehat{C_1}=\widehat{C_2}\left(t/c.phân.giác\right);\widehat{C_2}=\widehat{I_2}\left(so.le.trong.do.FI//BC\right)\)
\(\Rightarrow\widehat{C_1}=\widehat{I_1}\Rightarrow\Delta CFI.cân.tại.F\)
\(b,\) Vì \(\Delta BEI.và.\Delta CFI\) cân nên \(\left\{{}\begin{matrix}BE=EI\\CF=FI\end{matrix}\right.\)
\(\Rightarrow BE+CF=EI+FI=EF\)
Các hình thang: BEFC do EF//BC; ADFE do AE//DF; ABCD do giả thiết

Bài 2:
a: Xét ΔABE và ΔACF có
góc ABE=góc ACF
AB=AC
góc A chung
Do đó: ΔABE=ΔACF
Suy ra: AE=AF
b: Xét ΔABC có AF/AB=AE/AC
nên FE//BC
=>BFEC là hình thang
mà CF=BE
nên BFEC là hình thang cân
c: Xét ΔFEB có góc FEB=góc FBE
nên ΔFEB cân tại F
=>FE=FB=EC

A B C D O
Xét tam giác ABC và BAD có :
AB : chung
\(\widehat{BAD}=\widehat{ABC}\)
AD = BC
( ABCD là hình thang cân )
\(\Rightarrow\Delta ABC=\Delta BAD\)
\(\Rightarrow\widehat{BAC}=\widehat{ABD}\)
\(\Delta AOB\)CÓ : \(\widehat{OAB}=\widehat{OBA}\Rightarrow\Delta AOB\)cân tại O nên OA = OB