
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bạn đùa à? mũ 4 lên là bậc 8 đấy. bạn tìm cách khác cho mình với

chào tv mới
caua, 3x+x^2-4x=12
x^2-x-12=0
x^2-4x+3x-12=0
x(x-4)+3(x-4)=0
(x+3)(x-4)=0
x=-3 hoặc x=4
LƯU YS: từ chỗ mik biến đổi thành pt bậc 2 bn tính theo đenta cx đc, đây mik làm cách phân tích thành tích cho ngắn gọn


(x^2+6x+5)(x^2+6x+8)=10
Đặt x^2+6x+5=a>>>(a+3)a=10
a^2+3a-10=0 >>>(a+5)(a-2)=0>>>a=-5 hoặc a=2
Đến đây thay a =x^2+6x+5 ròi giải

b: Xét ΔAEB vuông tại E và ΔAKC vuông tại K có
\(\widehat{EAB}\) chung
Do đó: ΔAEB\(\sim\)ΔAKC
Suy ra: \(\dfrac{AE}{AK}=\dfrac{AB}{AC}\)
hay \(AK\cdot AB=AE\cdot AC\)

Bài 1:
a: ĐKXĐ: \(x\ge2\)
b: ĐKXĐ: \(x>\dfrac{1}{2}\)

4:
a: góc OBA+góc OCA=180 độ
=>OBAC nội tiếp
b: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA vuông góc BC tại H
=>AB^2=AH*AO
 giúp mình câu 4 với câu 2 phần 2 với
giúp mình câu 4 với câu 2 phần 2 với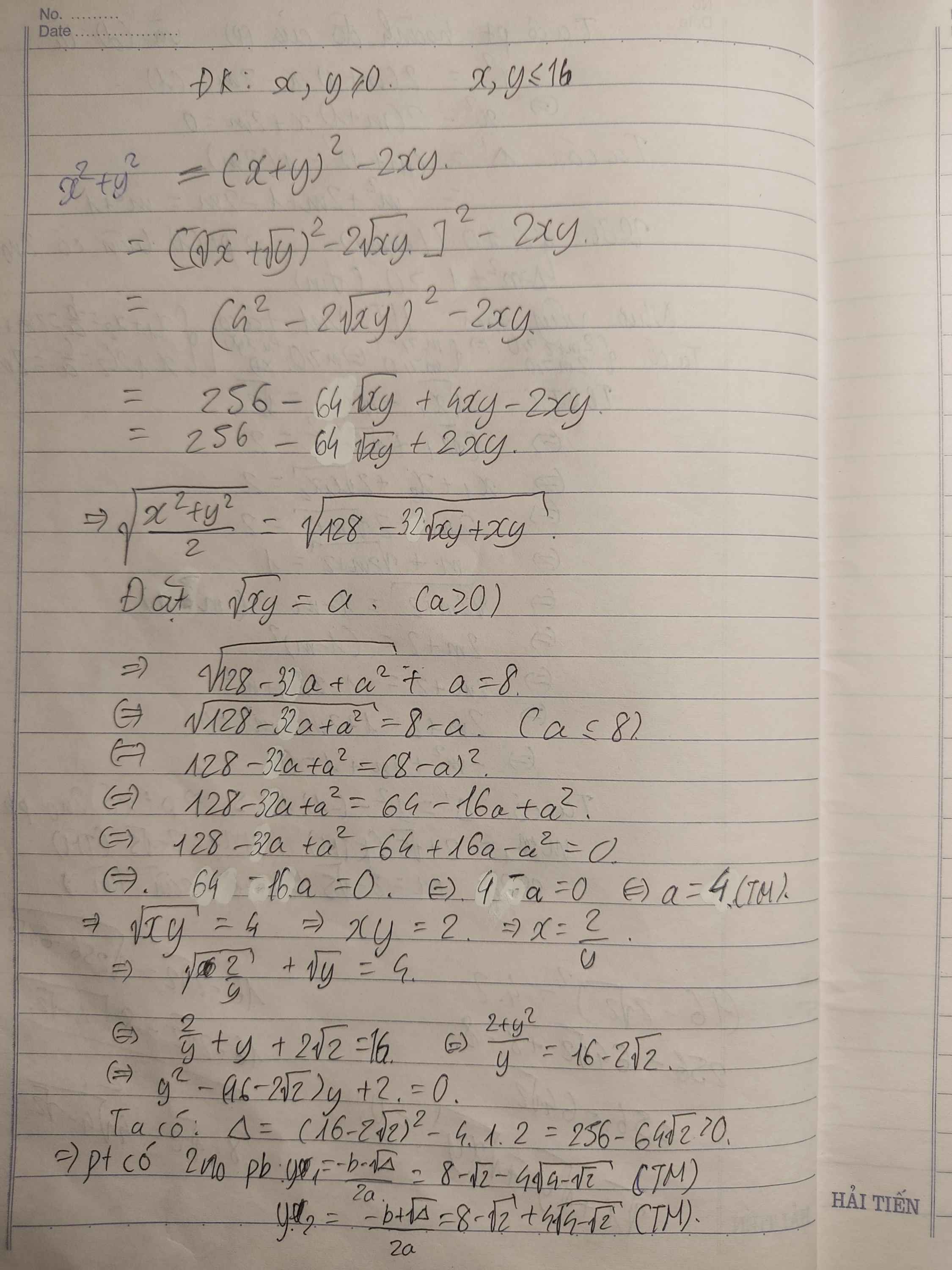
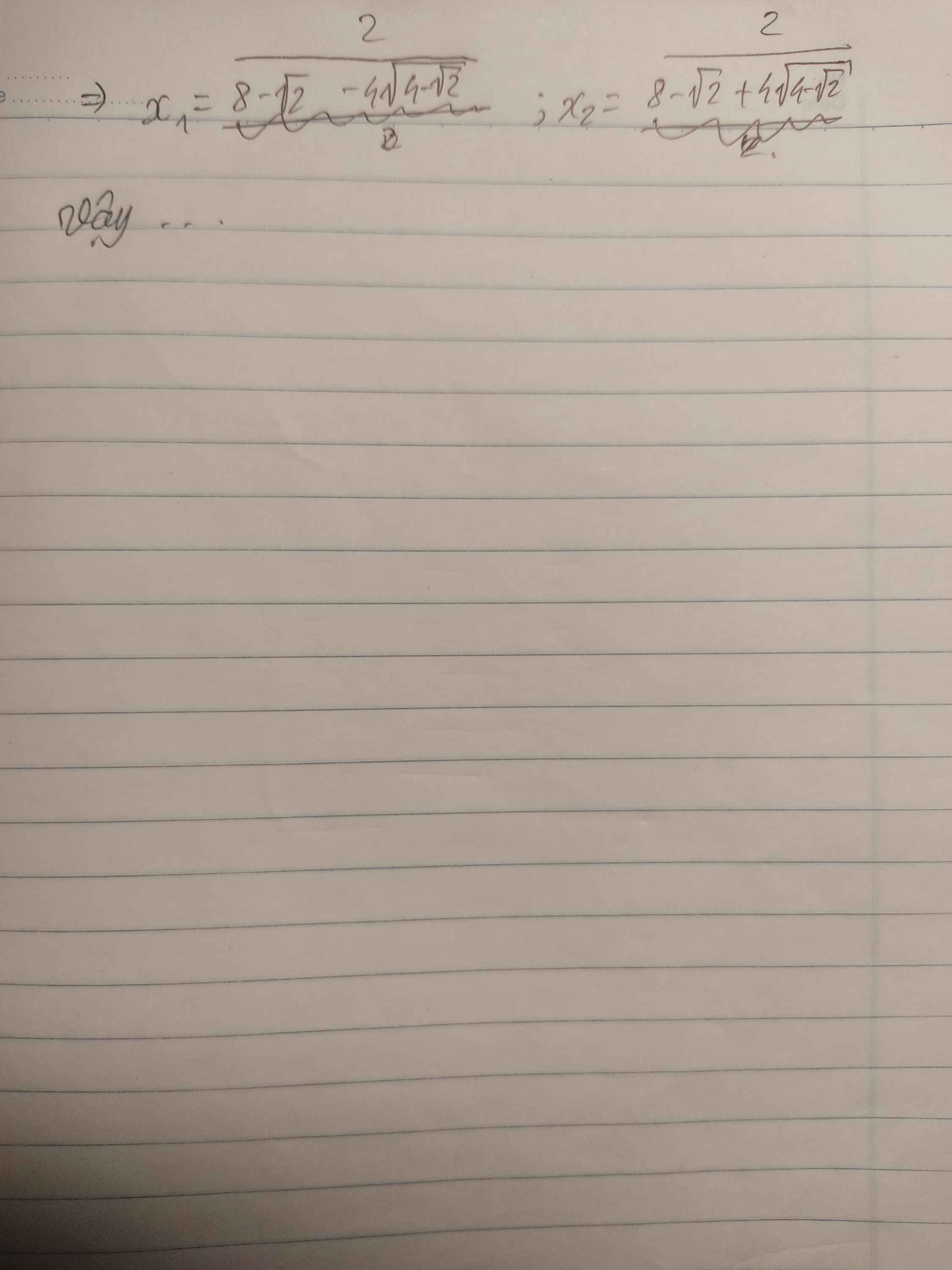


 Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!
Mọi người giúp mình câu 3, câu 4 với. Mình cảm ơn ạ. Mình đang cần gấp lắm!!!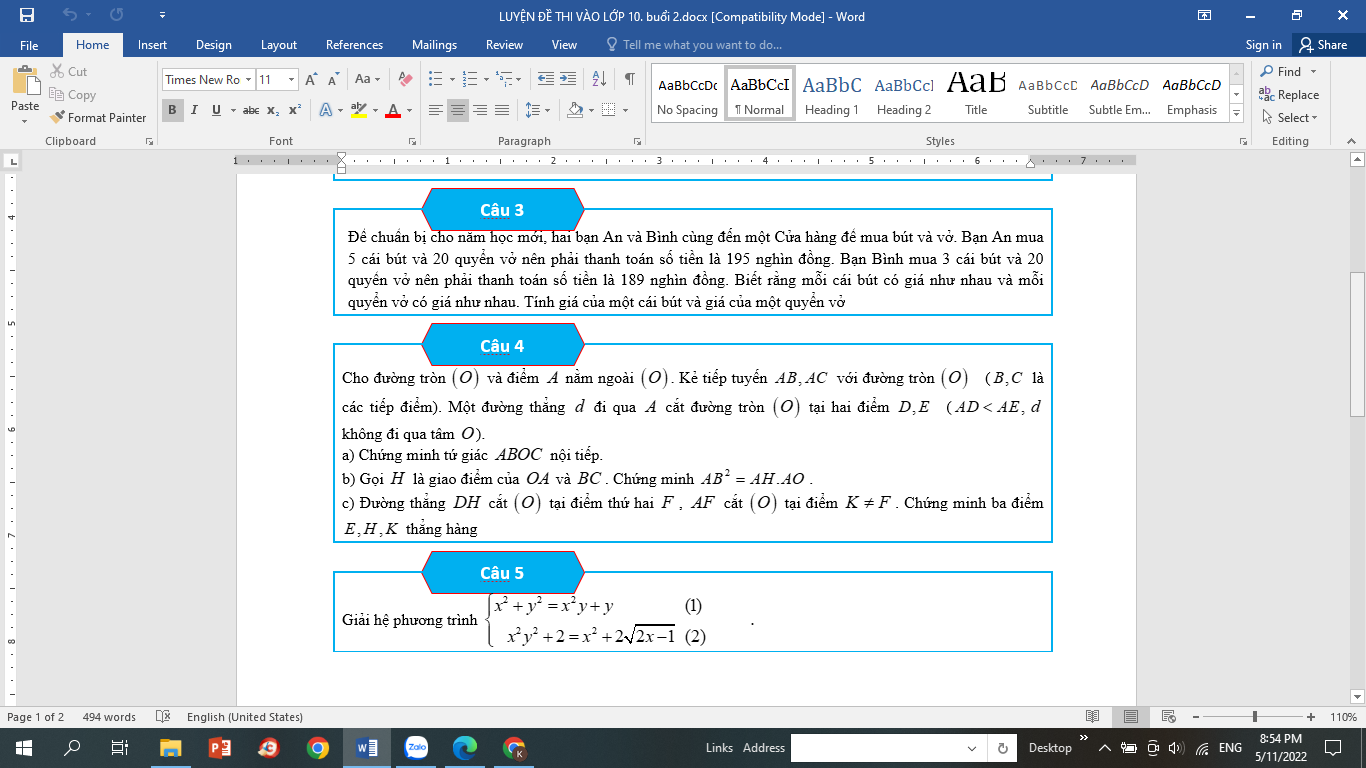
a, Vì AM; BM là tiếp tuyến đường tròn (O) với A;B là tiếp điểm
=> ^MAO = ^MBO = 900
Gọi I là trung điểm MO
Xét tam giác MAO vuông tại A, I là trung điểm MO
=> AI = MI = OI (1)
Xét tam giác MBO vuông tại B, I là trung điểm MO
=> BI = MI = OI (2)
Từ (1) ; (2) => A;B;M;O cùng thuộc 1 đường tròn
b, Vì MA = MB ( tc tiếp tuyến cắt nhau ) ; OA = OB = R
=> OM là đường trung trực
=> OM vuông AB
Ta có : ^ABC = 900 ( điểm thuộc đường tròn nhìn đường kính )
=> AB vuông BC
=> OM // BC ( tc vuông góc tới song song )
c, Ta có : OM // BC => ^MOB = ^OBC ( so le trong )
mà tam giác OBC cân vì OB = OC => ^OBC = ^OCB
=> ^MOB = ^OCB
Xét tam giác CKB và tam giác OBM ta có :
^CKB = ^OBM = 900
^KCB = ^MOB ( cmt )
Vậy tam giác CKB ~ tam giác OBM ( g.g )
\(\frac{CK}{OB}=\frac{BC}{OM}\Rightarrow CK.OM=BC.OB\)