Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giúp mình bài này với
bài 6 trong sách giáo khoa 6 tập một trang 55 ( một số bài toán về tỉ lệ thuận)

a) Vì khối lượng của cuộn dây thép tỉ lệ thuận với chiều dài nên y = kx.
Theo đề bàiy = 75 thì x = 3 thay vào công thức ta được 75 = k.3 hay k = 25.
Vậy k = 25x
b) Vì y = 25x nên khi y = 4,5kg = 4500g thì x = 4500: 25 = 180. Vậy cuộn dây dài 180m.

Gọi hai số cần tìm là \(a,b\)
\(\Rightarrow\frac{a}{b}=\frac{10}{15}=\frac{2}{3}\Rightarrow\frac{a}{2}=\frac{b}{3}\) và \(a+b=222,5\)
Áp dụng tính chất của dảy tỉ số bằng nhau ta có:
\(\frac{a}{2}=\frac{b}{3}=\frac{a+b}{2+3}=\frac{222,5}{5}=44,5\)
\(\Rightarrow\frac{a}{2}=44,5\Rightarrow a=44,5.2=89\)
\(\Rightarrow\frac{b}{3}=44,5\Rightarrow b=44,5.3=133,5\)

1.
a) Hai đại lượng x, y tỉ lệ thuận với nhau
b)Hai đại lượng x, y không tỉ lệ thuận với nhau

câu a và b đều điền vào chỗ trống là đối đỉnh
nhớ k cho mình nha!

Kẻ c//a qua O ⇒ c//b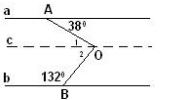
Ta có: a//c ⇒ ∠O1 = ∠A1 ( So le trong)
⇒ ∠O1 = 380
b//c ⇒ ∠O2 + ∠B1 = 1800 ( Hai góc trong cùng phía)
⇒ ∠O2 = 480
Vậy x = ∠O1 + ∠O2 = 380 + 480
x = 860

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{6}=\dfrac{c-a}{6-3}=14\)
Do đó: a=42; b=56; c=84
\(\text{Gọi x;y;z lần lượt là số sách lớp 7A,7B,7C:}\)
(đk:x;y;z\(\in\)N*,đơn vị:sách)
\(\text{Ta có:}\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{6}\text{ và }z-x=42\)
\(\text{Áp dụng tính chất dãy tỉ số bằng nhau:}\)
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{6}=\dfrac{z-x}{6-3}=\dfrac{42}{3}=14\)
\(\Rightarrow x=14.3=42\text{(sách)}\)
\(y=14.4=56\text{(sách)}\)
\(z=14.6=84\text{(sách)}\)
\(\text{Vậy số sách lớp 7A là: 42 sách}\)
\(\text{lớp 7B là:56 sách}\)
\(\text{lớp 7C là:84 sách}\)

Nếu : ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;
AM ≤ AC
+ Nếu M ≡ A hoặc M ≡ B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.
+ Nếu M nằm giữa B và C; ( M ≢ B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC
+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC
+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH
Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA
Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC
Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤ AB, AM ≤ AC
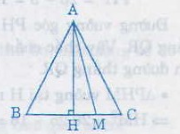
Giả sử ∆ABC cân tại A, M là điểm thuộc cạnh đáy BC, ta chứng minh AM ≤ AB;
AM ≤ AC
+ Nếu M ≡ A hoặc M ≡ B ( Kí hiệu đọc là trùng với) thì AM = AB, AM = AC.
+ Nếu M nằm giữa B và C; ( M ≢ B , C). Gọi H là trung điểm của BC, mà ∆ABC cân tại A nên AH ⊥ BC
+ Nếu M ≡ H => AM ⊥ BC => AM < AB và AM < AC
+ Nếu M ≢ K giả sử M nằm giữa H và C=> MH < CH
Vì MN và CH là hình chiếu MA và CA trên đường BC nên MA < CA => MA < BA
Chứng minh tương tự nếu M nằm giữa H và B thì MA < AB, MA < AC
Vậy mọi giá trị của M trên cạnh đáy BC thì AM ≤ AB, AM ≤ AC