K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 1 2024
a.
\(A=\left(\dfrac{\left(x-1\right)\left(x^2+x+1\right)}{x\left(x-1\right)}+\dfrac{\left(x-2\right)\left(x+2\right)}{x\left(x-2\right)}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+x+1}{x}+\dfrac{x+2}{x}+\dfrac{x-2}{x}\right):\dfrac{x+1}{x}\)
\(=\left(\dfrac{x^2+3x+1}{x}\right).\dfrac{x}{x+1}\)
\(=\dfrac{x^2+3x+1}{x+1}\)
2.
\(x^3-4x^3+3x=0\Leftrightarrow x\left(x^2-4x+3\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=1\left(loại\right)\\x=3\end{matrix}\right.\)
Với \(x=3\Rightarrow A=\dfrac{3^2+3.3+1}{3+1}=\dfrac{19}{4}\)
AH
Akai Haruma
Giáo viên
3 tháng 2 2024
Bài 4:
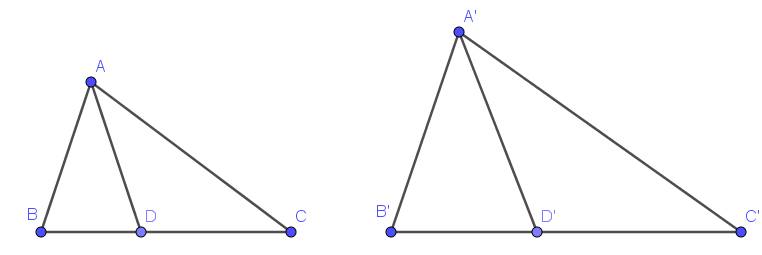
a. Vì $\triangle ABC\sim \triangle A'B'C'$ nên:
$\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{AC}{A'C'}(1)$ và $\widehat{ABC}=\widehat{A'B'C'}$
$\frac{DB}{DC}=\frac{D'B'}{D'C}$
$\Rightarrow \frac{BD}{BC}=\frac{D'B'}{B'C'}$
$\Rightarrow \frac{BD}{B'D'}=\frac{BC}{B'C'}(2)$
Từ $(1); (2)\Rightarrow \frac{BD}{B'D'}=\frac{BC}{B'C'}=\frac{AB}{A'B'}$
Xét tam giác $ABD$ và $A'B'D'$ có:
$\widehat{ABD}=\widehat{ABC}=\widehat{A'B'C'}=\widehat{A'B'D'}$
$\frac{AB}{A'B'}=\frac{BD}{B'D'}$
$\Rightarrow \triangle ABD\sim \triangle A'B'D'$ (c.g.c)
b.
Từ tam giác đồng dạng phần a và (1) suy ra:
$\frac{AD}{A'D'}=\frac{AB}{A'B'}=\frac{BC}{B'C'}$
$\Rightarrow AD.B'C'=BC.A'D'$
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 3 2023
Đặt \(a=\dfrac{1}{x};b=\dfrac{1}{y};c=\dfrac{1}{z}\Rightarrow xyz=1\) và \(x;y;z>0\)
Gọi biểu thức cần tìm GTNN là P, ta có:
\(P=\dfrac{1}{\dfrac{1}{x^3}\left(\dfrac{1}{y}+\dfrac{1}{z}\right)}+\dfrac{1}{\dfrac{1}{y^3}\left(\dfrac{1}{z}+\dfrac{1}{x}\right)}+\dfrac{1}{\dfrac{1}{z^3}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)}\)
\(=\dfrac{x^3yz}{y+z}+\dfrac{y^3zx}{z+x}+\dfrac{z^3xy}{x+y}=\dfrac{x^2}{y+z}+\dfrac{y^2}{z+x}+\dfrac{z^2}{x+y}\)
\(P\ge\dfrac{\left(x+y+z\right)^2}{y+z+z+x+x+y}=\dfrac{x+y+z}{2}\ge\dfrac{3\sqrt[3]{xyz}}{2}=\dfrac{3}{2}\)
\(P_{min}=\dfrac{3}{2}\) khi \(x=y=z=1\) hay \(a=b=c=1\)
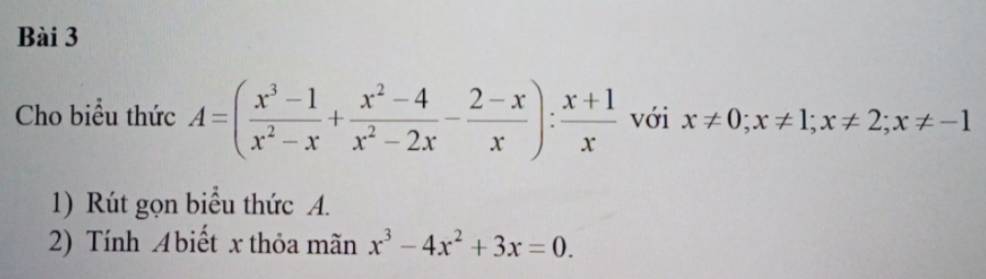
*NHỮNG DẤU IN ĐỎ LÀ KÍ HIỆU
BÀI 1:
a, khi x\(x\ge9\) thì A có dạng :
A= x-9+7=x-2
b, khi x≤0 thì B có dạng :
B=3x-8x^2+x-2=4x -8x^2 -2
C, Nhận xét : 2x+1=0óx=-1/2
4x=0óx=0
Lập bảng xét dấu
x
-1/2
0
/2x+1/
-(2X+1)
0 2X+1
II 2X+1
/4x/
-4X
II -4X
0 4X
Vs -1/2≤x≤0 thì biểu thức C có dạng :
C=5x +2x + 1+4x=11x+1
BÀI 2:
a , TH1: 3X-1=1/2
ó3X=1+1/2
ó3X=1,5
óX=0,5
TH2:3X-1=-1/2
ó3X=1-1/2
ó3X=0,5
óX=1/6
VẬY ......
b , Vì X^2≥-1 vs mọi x nên /x^2+1/=x^2+1, ta có pt:
3+2x+1=5
ó2x=5-1-3
ó2x=1
óx=0,5
Vậy ....
Phần c mk ko hiểu lắm d , Nếu 3x+4≥0óx≥-4/3 thì /3x+4/=3x+4
Ta có pt : 3x+4/2 -1 =1/3
ó(3x+4)3/2-6/6=2/6
ó9x+12-6=2
ó9x=2+6-12
ó9x=-4
óx=-4/9(t/m)
Nếu 3x+4≤0óx≤-4/3 thì /3x+4/=-3x-4
Ta có pt :-3x-4/2-1=1/3
ó3(-3x-4)/6 -6/6 =2/6
ó-9x -12-6=2
ó-9x=2+12+6
ó-9x=20
óx=-20/9(t/m)
VẬY....
BÀI 3: CT /x/=/y/ có 2 th :x=y và x=-y
a , TH1:4-5X=5-6X
ó-5X+6X=5-4
óX=1
TH2:4-5X=6X-5
ó-5X-6X=-5-4
ó-11X=-9
óX=11/9
VÂY...
b , /2X-2/-/7X+1/=0
ó/2X-2/=/7X+1/
TH1:2X-2=7X+1
ó2X-7X=1+2
ó-5X=3
óX=-3/5
TH2:2X-2= -7X-1
ó2X+7X=-1+2
ó9X=1
óX=1/9
VẬY ...
c , TH1:1/4(X-5)=3X+1
óX/4-5/4=3X+1
óX-5/4=4(3X+1)/4
óX-5=12X+4
óX-12X=4+5
ó-11X=9
óX=-9/11
TH2:1/4(X-5)=-3X-1
óX/4-5/4=4(-3X-1)/4
óX-5=-12X-4
óX+12X=-4+5
ó13X=1
óX=1/13
d ,KO CHÉP ĐỀ BÀI LM LUN NHÉ : ó /X^2-4/=-/X-2/
TH1:X^2-4=-X+2
óX^2+X-4-2=0
óX^+X-2=0
óX^2-X+2X-2=0
ó(X^2-X)+(2X-2)=0
óX(X-1)+2(X-1)=0
ó(X-1)(X+2)=0
óX-1=0 hoặc X+2=0
óX=1 hoặc X=-2
TH2:X^2-4=X-2
óX^2-X-4+2=0
óX^2-X-2=0
óX^2+X-2x-2=0
óX(X+1)-2(X+1)=0
ó(X+1)(X-2)=0
óX+1=0 hoặc X-2=0
óX=-1 hoặc X=2
VẬY ...
BÀI 4:
a , Nếu 2x+1≥0óx≥-1/2 thì /2x+1/=2x+1
Ta có pt :2x+1=x-2
ó2x-X=-2-1
óX=-3(LOẠI)
Nếu 2x+1≤0 óx≤-1/2 thì / 2x+1/= -2x-1
Ta có pt :-2x-1=x-2
ó-2x-x=-2+1
ó-3x=-1
óx=1/3(loại)
Vậy pt vô nghiệm
b , Nếu x-3≥0óx≥3 thì / x-3/=x-3
Ta có pt :x -3 -2=3x
óx-3x=2+3
ó-2x=5
óx=-5/2(loại)
Nếu x-3≤0óx≤3 thì /x-3/=3-x
Ta có pt : 3-x-2=3x
ó-x-3x=-3+2
ó-4x=-1
óx=1/4(t/m)
c , Nếu 5x≥0 óx≥0 thì /5x/=5x
Ta có pt : 5x=x-12
ó5x-x=-12
ó4x=-12
óx=-3 (loai)
Nếu 5x≤0 óx≤0 thì /5x/=-5x
Ta có pt : -5x=x-12
ó-5x-x=-12
ó-6x=-12
óx=2(loại)
VẬY PT VÔ NGHIỆM
phần còn lại tự lm nhé