
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x\left(x-\frac{1}{3}\right)< 0\)
Để \(x\left(x-\frac{1}{3}\right)< 0\)thì x và \(x-\frac{1}{3}\)trái dấu nhau
Thấy \(x>x-\frac{1}{3}\)\(\Rightarrow\hept{\begin{cases}x>0\\x-\frac{1}{3}< 0\end{cases}\Rightarrow\hept{\begin{cases}x>0\\x< \frac{1}{3}\end{cases}\Leftrightarrow}0< x< \frac{1}{3}}\)


A. TRẮC NGHIỆM (3 điểm)
I. Chọn một hoặc hai phương án trả lời đúng nhất. (2 điểm)
Câu 1: Đặc điểm nổi bật của khí hậu nhiệt đới gió mùa là:
A. Có thời kì khô hạn; B. Nhiệt độ và lượng mưa thay đổi theo mùa gió;
C. Thời tiết luôn diễn biến thất thường; D. Nắng nóng, mưa nhiều quanh năm;
Câu 2: Vấn đề cần quan tâm giải quyết ở đới lạnh đó là:
A. Thiếu nguồn nhân lực để phát triển kinh tế.; C. Ô nhiễm nguồn nước.
B. Ô nhiễm không khí. D. Nguy cơ tuyệt chủng một số loài động vật quý.
Câu 3: Cảnh quan môi trường nhiệt đới thay đổi về chí tuyến theo thứ tự:
A. Rừng thưa, xa van, nửa hoang mạc. B. Nửa hoang mạc, rừng thưa, xa van.
C. Xa van, nửa hoang mạc, rừng thưa. D. Rừng thưa, nửa hoang mạc, xa van
Câu 4: Rừng rậm xanh quanh năm là loại rừng chính thuộc:
A. Môi trường nhiệt đới B. Môi trường xích đạo ẩm
C. Môi trường nhiệt đới gió mùa. D. Môi trường hoang mạc
II. Dựa vào kiến thức đã học hãy điền từ (hoặc cụm từ) vào ô trống (1 điểm)
Ở đới ôn hòa thiên nhiên phân hóa theo......(1)........một năm có bốn mùa Xuân, Hạ, Thu, Đông. Các kiểu môi trường cũng thay đổi từ Bắc xuống Nam là do... (2)...., thay đổi từ Tây sang Đông do ảnh hưởng của......(3).....và.....(4)..........
B. TỰ LUẬN (7 điểm)
Câu 1: (2,5 điểm) Nêu vị trí, đặc điểm môi trường nhiệt đới? Nước ta thuộc kiểu môi trường nào?
Câu 2: (2 điểm) Trình bày đặc điểm về hình dạng, địa hình và khoáng sản của châu Phi?
Câu 3: (2,5 điểm) Nêu những nguyên nhân và hậu quả của ô nhiễm nước ở đới ôn hòa? Liên hệ ở địa phương về tình trạng này?
Câu 4: (1 điểm). Dành cho lớp A, B, câu 1, 3 tính 2đ/câu.
Qua bảng số liệu dưới đây (nhiệt độ, lượng mưa trung bình tháng), em hãy xác định địa điểm này thuộc môi trường địa lí nào trên Trái Đất? Giải thích?
Tháng | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Nhiệt độ (0C) | 25 | 25 | 26 | 27 | 28 | 25 | 26 | 27 | 27 | 28 | 25 | 25 |
Lượng mưa: mm | 45 | 50 | 90 | 135 | 350 | 400 | 220 | 60 | 70 | 170 | 200 | 100 |
Có đáp án:
A. TRẮC NGHIỆM: (3 điểm)
I. Chọn một hoặc hai phương án trả lời đúng nhất. (2 điểm)
Câu 1: B, C (0,5đ). Câu 2: A, D. (0,5đ)
Câu 3: A (0,5đ); Câu 4: B (0,5đ)
* Lưu ý: HS chọn được 2 ý, mỗi ý đúng thì được 0,25đ, nếu chọn 1, 3, 4, 5 ý thì không cho điểm dù có 2 ý đúng.
II. Điền vào ô trống những nội dung kiến thức cho phù hợp: (mỗi ý trả lời đúng 0,25đ)
(1) thời gian; (2) vĩ độ;
(3) dòng biển; (4) gió tây ôn đới.
B. TỰ LUẬN (7 điểm)
Câu 1: HS trả lời được các ý sau
- Môi trường nhiệt đới:
- Vị trí: Nằm ở khoảng 50B và 50N đến chí tuyến ở 2 bán cầu. (0,5đ)
- Đặc điểm:
- Nóng quanh năm, có thời kì khô hạn, càng gần chí tuyến thời kì khô hạn càng kéo dài, biên độ nhiệt trong năm càng lớn. (0,5đ)
- Lượng mưa và thảm thực vật thay đổi từ xích đạo về chí tuyến. (0,5đ)
- Nước ta thuộc kiểu môi trường nhiệt đới gió mùa. (0,5đ)
Câu 2: HS trả lời được các ý sau
- Hình dạng: châu Phi có dạng hình khối (0,25đ), đường bờ biển ít bị chia cắt, rất ít vịnh biển, bán đảo, đảo. (0,25đ)
- Địa hình: tương đối đơn giản (0,25đ), có thể coi toàn bộ châu lục là khối sơn nguyên lớn. (0,25đ)
- Khoáng sản: nguồn khoáng sản phong phú (0,25đ), nhiều kim loại quý, hiếm (vàng, kim cương, u-ra-ni-um...) (0,25đ)
Câu 3: HS trả lời được các ý sau
- Nguyên nhân:
- Ô nhiễm biển là do váng dầu, các chất độc hại bị đưa ra biển. (0,25đ)
- Ô nhiễm nước sông, hồ và nước ngầm là do hoá chất thải ra từ các nhà máy, lượng phân hoá học và thuốc trừ sâu dư thừa trên đồng ruộng, cùng các chất thải nông nghiệp. (0,25đ)
- Hậu quả:
- Làm chết ngạt các sinh vật sống trong nước. (0,25đ)
- Thiếu nước sạch cho đời sống và sản xuất. (0,25đ)
- Liên hệ được: chất thải, rác thải ra sông, suối... nông dân phun thuốc trừ sâu trên đồng ruộng...(1đ)
Câu 4:
- HS nhận dạng đúng môi trường xích đạo ẩm. (0,5đ)
- Giải thích: vì nhiệt độ trung bình năm 250C, biên độ nhiệt năm thấp 30C, mưa quanh năm, lượng mưa trung bình năm trên 1500mm. (1đ)

A. Trắc nghiệm: (3đ)
Bài 1: Em hãy khoanh tròn vào chữ cái đầu câu trả lời đúng duy nhất trong các câu sau(1đ)
Câu 1. Vì sao sứa thích nghi được với đời sống di chuyển tự do?
A. Cơ thể có nhiều tua.
B. Ruột dạng túi.
C. Cơ thể hình dù, có tầng keo dày để dễ nổi, lỗ miệng quay xuống dưới.
D. Màu sắc cơ thể sặc sỡ.
Câu 2. Động vật đa dạng phong phú nhất ở vùng nào?
A. Vùng ôn đới B. Vùng Bắc cực C. Vùng Nam cực D. Vùng nhiệt đới
Câu 3: Giun đũa là sinh vật phân tính hay lưỡng tính?
A. Lưỡng tính B. Phân tính C. Lưỡng tính hoặc phân tính D. Cả a,b và c
Câu 4: Ruột khoang có số lượng khoảng?
A. 20.000 loài B. 15.000 loài C. 10.000 loài D. 5.000 loài
Bài 2: Tìm các cụm từ phù hợp điền vào chỗ trống (1đ)
Trùng roi xanh là một cơ thể động vật(1)......................, di chuyển nhờ roi, vừa(2)......................... vừa dị dưỡng, hô hấp qua màng(3)........................., bài tiết và điều chỉnh áp suất thẩm thấu nhờ không bào co bóp, sinh sản vô tính theo cách(4).........................
Bài 3: Nối cột A với B: (1đ)
1. Sán lá máu | a. Kí sinh trong ốc ruộng | |
2. Sán lá gan | b. Kí sinh ruột non người | |
3. Sán bã trầu | c. Kí sinh ở ruột lợn | |
4. Sán dây | d. Kí sinh trong máu người |
B. Tự luận (7đ)
Câu 1: Điểm giống nhau và khác nhau giữa động vật và thực vật là gì? (2.5đ)
Câu 2: Trình bày nơi sống, cấu tạo, di chuyển, dinh dưỡng, sinh sản của sán lá gan? Mô tả vòng đời của sán lá gan. (2.5đ)
Câu 3: Tại sao người bị sốt rét khi đang sốt nóng cao mà người lại rét run cầm cập? (1đ)
Câu 4: Vì sao khi mưa nhiều giun đất lại chui lên mặt đất. (1đ)
Câu hỏi trắc nghiệm
(3 điểm)
Câu 1. Nhóm nào dưới đây gồm những động vật sống trên cạn?
A, hổ, sứa, mực, cáo.
B. đại bàng, muỗi, hến, ngựa.
C. linh dương, khỉ, diều hâu, cá.
D. gà, chó, nai, thỏ.
Câu 2. Hãy chú thích thay cho các số trong hình dưới đây
Chú thích
1 - …………….
2 - …………….
3 - …………….
4 - …………….
Câu 3. Hãy chú thích thay cho các số trong hình sau
Chú thích
1 - ………………
2 - ………………
Câu 4. Cá chép hô hấp bằng
A. mang. B. phổi.
C. hệ thống ống khí. D. da.
Câu 5. Hiện nay ở Việt Nam có khoảng bao nhiêu loài cá?
A. 850. B. 25415. C. 2753. D. 24565.
Câu hỏi tự luận
(7 điểm)
Câu 1. Em hãy kể tên 10 loài động vật ở xung quanh nơi em đang sống và chỉ rõ nơi cư trú của chúng?
Câu 2. Trong dân gian có một vài tin đồn về khả năng “tái sinh vô hạn” của đỉa. Tức là nếu cắ t đỉa ra làm nhiều phần thì mỗi phần sẽ phát triển thành 1 cơ thể mới. Với góc nhìn khoa học, theo em ta có thể giết chểt hoàn toàn 1 con đỉa không? Giết bằng cách nào?
Câu 3: Trình bày đặc điểm chung của lớp Sâu bọ. Trong số các đặc điểm chung của Sâu bọ, đặc điểm nào phân biệt chúng với các Chân khớp khác?
Câu 4. Có nên ăn trai sông ở vùng nước ô nhiễm không? Vì sao?
Câu 5. Mài mặt ngoài của trai ngửi thấy có mùi khét? Vì sao?
Đáp án
Câu hỏi trắc nghiệm
Câu 1: D
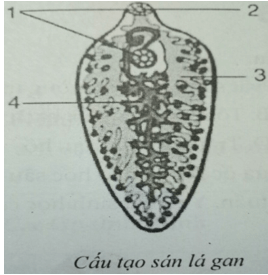
Câu 2:
Chú thích
1- Giác bám
2- Miệng
3- Nhánh ruột
4- Cơ quan sinh dục lưỡng tính (phân nhánh)
Cấu tạo sán lá gan
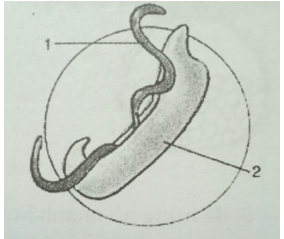
Câu 3:
Chú thích
1- Con cái
2- Con đực
Câu 4: A Câu 5: C
Câu hỏi tự luận
Câu 1.
| STT | Tên động vật | Nơi cư trú |
| 1 | Chuột | Cống, hang chuột,.. |
| 2 | Cá | Ao, hồ, sông, suối, biển, đồng ruộng, mương, máng |
| 3 | Mèo | Rừng, chuồng mèo |
| 4 | Chó | Rừng, chuồng chó |
| 5 | Ốc | Ao, hồ, sông, suối, biển, đồng ruộng, mương, máng |
| 6 | Muỗi | Nơi tối, bụi cây, vũng nước đọng |
| 7 | Ong | Tổ ong |
| 8 | Chim | Làm tổ trên cây |
| 9 | Ếch | Ao, đầm, sông, suối,… |
| 10 | Gà | Rừng, chuồng gà |
Câu 2.
Với góc nhìn khoa học, ta hoàn toàn có thể giết chết đỉa bằng một trong các cách sau:
- Cắt theo chiều dọc (hình thức phá vỡ thể xoang).
- Bằng môi trường cồn.
- Môi trường có nồng độ muối/ axit/ bazơ cao.
- Nhiệt (đỉa sẽ chết hoàn toàn nếu bị đốt cháy, nhiệt do phản ứng nước với vôi,…), dân gian Việt Nam có câu: “Như đỉa phải vôi”.
Câu 3.
- Đặc điểm chung của lớp Sâu bọ:
+ Cơ thể sâu bọ có 3 phần: đầu, ngực, bụng.
+ Phần đầu có 1 đôi râu, phần ngực có 3 đôi chân và 2 đôi cánh.
+ Hô hấp bằng hệ thống ống khí.
- Trong các đặc điểm trên, đặc điểm nổi bật giúp phân biệt Sâu bọ với các Chân khớp khác là: phần đầu có 1 đôi râu, phần ngực có 3 đôi chân và 2 đôi cánh.
Câu 4.
- Chúng ta không nên ăn trai sống ở những vùng nước bị ô nhiễm. Vì trai sống ở những vùng nước bị ô nhiễm, khi trai lọc nước (để tìm thức ăn) nhiều chất độc hại sẽ nhiễm vào cơ thể trai, do đó người ăn phải trai này sẽ bị ngộ độc.
Câu 5.
Mài mặt ngoài của vỏ trai ngửi thấy có mùi khét là vì phía ngoài là lớp sừng có thành phần giống tổ chức sừng ở các động vật khác nên khi mài nóng cháy, chúng có mùi khét.

Ta có: |x - 3| + |x - 5| \(\ge\)|x - 3 + x - 5| = |2x - 8| = 2x - 8 (đk: x \(\ge\)4 => x - 4 \(\ge\)0)
Dấu "=" xảy ra <=> (x - 3)(x - 5) \(\ge\)0
Do x - 4 \(\ge\)0 => x - 3 > 0
=> x - 5 \(\ge\)0 => x \(\ge\)5
Vậy x \(\ge\)5 thì tmđb

Sao không viết câu hỏi ra đây luôn đi chứ có thể nhièu người biết mà không có sách lắm! Sao hướng dẫn được


a, XÉT TAM GIÁC AKO VÀ TAM GIÁC NBO CÓ :
AO=NO
KO=BO
GÓC AOK = GÓC BON
---> TAM GIÁC AKO = TAM GIÁC NBO ( C.G.C)
b, VÌ TAM GIÁC AKO = TAM GIÁC NBO :
---> GÓC AKO = GÓC NBO
MÀ 2 GÓC NÀY Ở VỊ TRÍ SO LE TRONG
---> AK // BN
c, XÉT TAM GIÁC ABO VÀ TAM GIÁC NKO :
AO = ON
GÓC AOB = GÓC NOK
OK = OB
---> TAM GIÁC ABO = TAM GIÁC NKO ( C.G.C)
---> AB = KN
---> GÓC ABO = GÓC NKO
MÀ 2 GÓC NÀY Ở VỊ TRÍ SO LE TRONG
---> AB//KN
NHỚ TiiCK NHA NHÓC
a) Xét \(\Delta AKO\)và \(\Delta NBO\)có :
\(\hept{\begin{cases}AO=NO\left(gt\right)\\KO=BO\left(gt\right)\\AOK=NOB\left(đđ\right)\end{cases}\Leftrightarrow\Delta AKO=\Delta NBO\left(c.g.c\right)}\)
b) Theo câu a ta có \(\Delta AKO=\Delta NBO\)suy ra góc KAO = góc BNO suy ra AK song song BN ( Vì có 2 góc so le trong bằng nhau )
c) Tương tự câu a chứng minh được \(\Delta AOB=\Delta NOK\left(c.g.c\right)\Rightarrow AB=NK;ABO=NKO\)suy ra AB song sonh NK vì có 2 góc so le trong bằng nhau