
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
Vận tốc cano khi dòng nước lặng là: $25-2=23$ (km/h)
Bài 2:
Đổi 1 giờ 48 phút = 1,8 giờ
Độ dài quãng đường AB: $1,8\times 25=45$ (km)
Vận tốc ngược dòng là: $25-2,5-2,5=20$ (km/h)
Cano ngược dòng từ B về A hết:
$45:20=2,25$ giờ = 2 giờ 15 phút.

Bài 1:
a.
$a^3-a^2c+a^2b-abc=a^2(a-c)+ab(a-c)$
$=(a-c)(a^2+ab)=(a-c)a(a+b)=a(a-c)(a+b)$
b.
$(x^2+1)^2-4x^2=(x^2+1)^2-(2x)^2=(x^2+1-2x)(x^2+1+2x)$
$=(x-1)^2(x+1)^2$
c.
$x^2-10x-9y^2+25=(x^2-10x+25)-9y^2$
$=(x-5)^2-(3y)^2=(x-5-3y)(x-5+3y)$
d.
$4x^2-36x+56=4(x^2-9x+14)=4(x^2-2x-7x+14)$
$=4[x(x-2)-7(x-2)]=4(x-2)(x-7)$
Bài 2:
a. $(3x+4)^2-(3x-1)(3x+1)=49$
$\Leftrightarrow (3x+4)^2-[(3x)^2-1]=49$
$\Leftrightarrow (3x+4)^2-(3x)^2=48$
$\Leftrightarrow (3x+4-3x)(3x+4+3x)=48$
$\Leftrightarrow 4(6x+4)=48$
$\Leftrightarrow 6x+4=12$
$\Leftrightarrow 6x=8$
$\Leftrightarrow x=\frac{4}{3}$
b. $x^2-4x+4=9(x-2)$
$\Leftrightarrow (x-2)^2=9(x-2)$
$\Leftrightarrow (x-2)(x-2-9)=0$
$\Leftrightarrow (x-2)(x-11)=0$
$\Leftrightarrow x-2=0$ hoặc $x-11=0$
$\Leftrightarrow x=2$ hoặc $x=11$
c.
$x^2-25=3x-15$
$\Leftrightarrow (x-5)(x+5)=3(x-5)$
$\Leftrightarrow (x-5)(x+5-3)=0$
$\Leftrightarrow (x-5)(x+2)=0$
$\Leftrightarrow x-5=0$ hoặc $x+2=0$
$\Leftrightarrow x=5$ hoặc $x=-2$


a)tam giác BHA có BI là phân giác(góc ABI=góc HBI) nên \(\dfrac{AI}{IH}=\dfrac{AB}{BH}\Rightarrow AI\cdot BH=AB\cdot IH\)
b)xét tam giác BHA và tam giác BAC có:
góc ABC chung
góc BHA=góc BAC=90 độ
\(\Rightarrow\Delta BHA\infty\Delta BAC\left(g.g\right)\\ \Rightarrow\dfrac{BH}{AB}=\dfrac{AB}{BC}\Rightarrow AB^2=BH\cdot BC\)
c)ta có:
theo câu a) \(\dfrac{AI}{IH}=\dfrac{AB}{BH}\Rightarrow\dfrac{IH}{AI}=\dfrac{BH}{AB}\left(1\right)\)
theo câu b) \(\dfrac{BH}{AB}=\dfrac{AB}{BC}\)
ta lại có BD là phân giác góc ABC nên \(\dfrac{AB}{BC}=\dfrac{AD}{DC}\Rightarrow\dfrac{AD}{DC}=\dfrac{BH}{AB}\)(2)
từ (1) và (2)\(\Rightarrow\dfrac{IH}{IA}=\dfrac{AD}{DC}\left(=\dfrac{BH}{AB}\right)\)


Xét tứ giác ABEC có
AB//EC
AC//BE
Do đó: ABEC là hình bình hành
Suy ra: AC=BE
mà AC=BD
nên BE=BD
hay ΔBED cân tại B


\(a,\left|x+3,4\right|+\left|x+2,4\right|+\left|x+7,2\right|=4x\)
\(\left|x+3,4\right|\ge0;\left|x+2,4\right|\ge0;\left|x+7,2\right|\ge0\)
\(< =>\left|x+3,4\right|+\left|x+2,4\right|+\left|x+7,2\right|>0\)
\(< =>4x>0\)
\(x>0\)
\(\hept{\begin{cases}\left|x+3,4\right|=x+3,4\\\left|x+2,4\right|=x+2,4\\\left|x+7,2\right|=x+7,2\end{cases}}\)
\(x+3,4+x+2,4+x+7,2=4x\)
\(x=13\left(TM\right)\)
\(b,3^{n+3}+3^{n+1}+2^{n+3}+2^{n+2}\)
\(3^n.27+3^n.3+2^n.8+2^n.4\)
\(3^n.30+2^n.12\)
\(\hept{\begin{cases}3^n.30⋮6\\2^n.12⋮6\end{cases}}\)
\(< =>3^n.30+2^n.12⋮6< =>VP⋮6\)
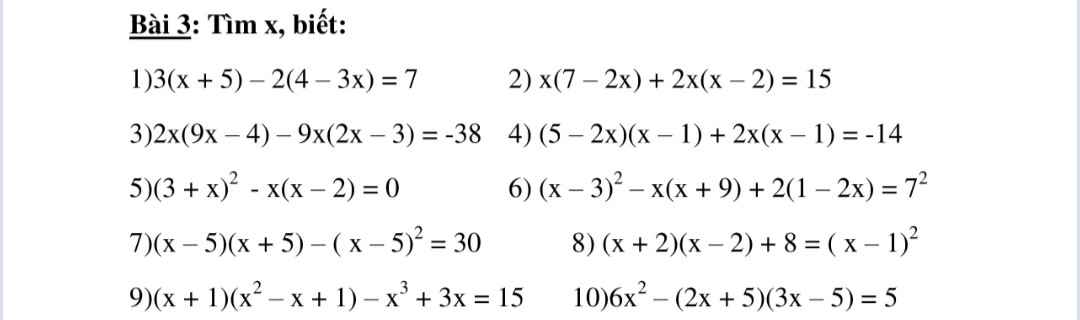




 giúp mk nha mờn nhìu ạk
giúp mk nha mờn nhìu ạk


 cac
cac giúp mik với nha!
giúp mik với nha!

 Giup mik voi
Giup mik voi


1: Ta có: \(3\left(x+5\right)-2\left(4-3x\right)=7\)
\(\Leftrightarrow3x+15-8+6x=7\)
\(\Leftrightarrow9x=14\)
hay \(x=\dfrac{14}{9}\)
2: Ta có: \(x\left(7-2x\right)+2x\left(x-2\right)=15\)
\(\Leftrightarrow7x-2x^2+2x^2-4x=15\)
\(\Leftrightarrow3x=15\)
hay x=5
3: Ta có: \(2x\left(9x-4\right)-9x\left(2x-3\right)=-38\)
\(\Leftrightarrow18x^2-8x-18x^2+27x=-38\)
\(\Leftrightarrow19x=-38\)
hay x=-2
7: Ta có: \(\left(x-5\right)\left(x+5\right)-\left(x-5\right)^2=30\)
\(\Leftrightarrow x^2-5-x^2+10x-25=30\)
\(\Leftrightarrow10x=60\)
hay x=6
8: Ta có: \(\left(x+2\right)\left(x-2\right)+8=\left(x-1\right)^2\)
\(\Leftrightarrow x^2-4+8=x^2-2x+1\)
\(\Leftrightarrow-2x=3\)
hay \(x=-\dfrac{3}{2}\)