
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


gọi \(x\) là độ dài cạnh hình vuông
\(\Rightarrow\) diện tích hình vuông ban đầu là \(x^2\)
đội dài cạnh hình vuông lúc sau là \(x+2\)
\(\Rightarrow\) diện tích hình vuông lúc sau là \(\left(x+2\right)^2\)
vì sau khi thay đổi thì diện tích hình vuông đó tăng thêm \(32m^2\) nên ta có phương trình
\(x^2+32=\left(x+2\right)^2\Leftrightarrow x^2+32=x^2+4x+4\)
\(\Leftrightarrow\) \(4x+4-32=0\Leftrightarrow4x-28=0\Leftrightarrow4x=28\)
\(\Leftrightarrow\) \(x=\dfrac{28}{4}=7\)
vậy diện tích lúc đầu của hình vuông là \(x^2=7^2=49\)\(m^2\)
Bài tui sai tiếp ak!
Tuấn Anh Phan Nguyễn a xóa giúp e zới! Nhất định hậu tạ!



1) Vì ∠xOt và ∠tOy là 2 góc kề bù nên
∠xOt + ∠tOy = 180°
=> ∠xOt = 180° - ∠tOy
∠xOt = 180° - 60°
∠xOt = 120°
Vậy ∠xOt = 120°
3,Om là tia phân giác của yot
=>mOt=\(30^0\)
On là tia phân giác của xOt
=>nOt=\(60^0\)
Om là tia phân giác của yOt
On là tia phân giác của xOt
=>Ot nằm giữa Om,On
nOt+mOt=nOm
nOm=30+60=90
=>......................

\(\Rightarrow\dfrac{5}{4}-\dfrac{1}{4}x=\dfrac{3}{10}x-\dfrac{2}{5}\)
\(\Rightarrow\dfrac{5}{4}+\dfrac{2}{5}=\dfrac{3}{10}x-\dfrac{1}{4}x\)
\(\Rightarrow\dfrac{33}{20}=\dfrac{11}{20}x\)
\(\Rightarrow x=\dfrac{33}{20}\div\dfrac{11}{20}\)
\(\Rightarrow x=3\)
\(1\dfrac{1}{4}-x\dfrac{1}{4}=x\cdot30\%\cdot\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{5}{4}-x\dfrac{1}{4}=x\cdot\dfrac{3}{10}-\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{5}{4}-\dfrac{1}{4}x=\dfrac{3}{10}x-\dfrac{2}{5}\)
\(\Leftrightarrow25-5x=6x-8\)
\(\Leftrightarrow-5x-6x=-8-25\)
\(\Leftrightarrow-11x=-33\)
\(\Leftrightarrow x=3\)
Vậy x = 3




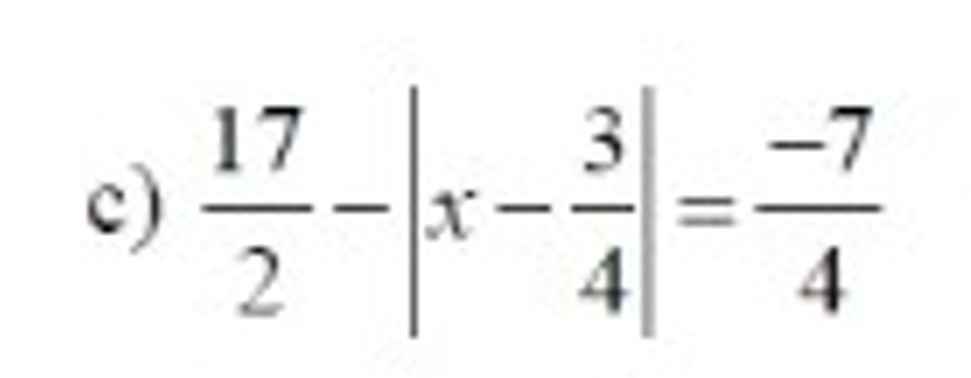 giúp mik nhé mọi người ơi
giúp mik nhé mọi người ơi








 Làm giúp tui nhé cảm ơn mọi người rất nhìu !
Làm giúp tui nhé cảm ơn mọi người rất nhìu !
 giúp mình với mọi người ơi mình xin đó
giúp mình với mọi người ơi mình xin đó
\(\Leftrightarrow\left|x-\dfrac{3}{4}\right|=\dfrac{17}{2}+\dfrac{7}{4}=\dfrac{41}{4}\)
\(\Leftrightarrow x-\dfrac{3}{4}\in\left\{\dfrac{41}{4};-\dfrac{41}{4}\right\}\)
hay \(x\in\left\{11;-\dfrac{19}{2}\right\}\)
\(\left|x-\dfrac{3}{4}\right|=\dfrac{41}{4}\)
TH1 : \(x-\dfrac{3}{4}=\dfrac{41}{4}\Leftrightarrow x=\dfrac{44}{4}=11\)
TH2 : \(x-\dfrac{3}{4}=-\dfrac{41}{4}\Leftrightarrow x=-\dfrac{38}{4}=-\dfrac{19}{2}\)