K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
KS
0
2N
7
ND
mn giúp mik vs mik cần gấp( có trình bày nha~)
1
15 tháng 12 2021
Gọi thời gian của T,D,M lần lượt là \(a,b,c(giờ;a,b,c>0)\)
Áp dụng tc dtsbn:
\(10a=9b=8c\Leftrightarrow\dfrac{10a}{360}=\dfrac{9b}{360}=\dfrac{8c}{360}\Leftrightarrow\dfrac{a}{36}=\dfrac{b}{40}=\dfrac{c}{45}=\dfrac{c-a}{45-36}=\dfrac{0,3}{9}=\dfrac{1}{30}\\ \Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{6}{5}\\b=\dfrac{4}{3}\\c=\dfrac{3}{2}\end{matrix}\right.\)
Vậy ...
DL
2
5 tháng 1 2022
\(\text{Bài 1:a)}25\dfrac{3}{19}.\left(-\dfrac{4}{5}\right)-35\dfrac{3}{19}.\left(-\dfrac{4}{5}\right)\)
\(=\dfrac{478}{19}.\left(-\dfrac{4}{5}\right)-\dfrac{668}{19}.\left(-\dfrac{4}{5}\right)\)
\(=\left(-\dfrac{4}{5}\right).\left(\dfrac{478}{19}-\dfrac{668}{19}\right)\)
\(=\left(-\dfrac{4}{5}\right).\left(\dfrac{-190}{19}\right)\)
\(=\left(-\dfrac{4}{5}\right).\left(-10\right)=8\)
\(\text{b)}5:\left(-\dfrac{5}{2}\right)^2+\dfrac{2}{15}.\sqrt{\dfrac{9}{4}}-\left(-2021\right)^0+0,25\)
\(=5:\dfrac{25}{4}+\dfrac{2}{15}.\dfrac{3}{2}-1+\dfrac{1}{4}\)
\(=\dfrac{4}{5}+\dfrac{1}{5}-1+\dfrac{1}{4}\)
\(=1-1+\dfrac{1}{4}\)
\(=0+\dfrac{1}{4}=\dfrac{1}{4}\)
\(\text{Bài 2:a)}\dfrac{8}{5}-\dfrac{3}{5}:x=0,4\)
\(\dfrac{3}{5}:x=\dfrac{8}{5}-0,4=\dfrac{6}{5}\)
\(x=\dfrac{3}{5}.\dfrac{5}{6}=\dfrac{1}{2}\)
\(\text{b)}\left(3x-\dfrac{1}{2}\right)^2+\dfrac{21}{25}=1\)
\(\left(3x-\dfrac{1}{2}\right)^2\) \(=1-\dfrac{21}{25}=\dfrac{4}{25}=\pm\left(\dfrac{2}{5}\right)^2\)
\(\text{Vậy }3x-\dfrac{1}{2}=\dfrac{2}{5}\)
\(3x\) \(=\dfrac{2}{5}+\dfrac{1}{2}=\dfrac{9}{10}\)
\(x\) \(=\dfrac{9}{10}.\dfrac{1}{3}=\dfrac{3}{10}\)
\(\text{hoặc }3x-\dfrac{1}{2}=\dfrac{-2}{5}\)
\(3x\) \(=\left(\dfrac{-2}{5}\right)+\dfrac{1}{2}=\dfrac{1}{10}\)
\(x\) \(=\dfrac{1}{10}.\dfrac{1}{3}=\dfrac{1}{30}\)
\(\Rightarrow x\in\left\{\dfrac{3}{10};\dfrac{1}{30}\right\}\)
5 tháng 1 2022
Bài 2:
a: =>3/5:x=6/5
hay x=3/5:6/5=1/2
b: \(\Leftrightarrow\left(3x-\dfrac{1}{2}\right)^2=\dfrac{4}{5}\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-\dfrac{1}{2}=\dfrac{2}{5}\\3x-\dfrac{1}{2}=-\dfrac{2}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{10}\\x=\dfrac{1}{30}\end{matrix}\right.\)
4 tháng 12 2021
\(\left\{{}\begin{matrix}\widehat{OAB}=\widehat{ODC}\left(AB\text{//}CD\right)\\\widehat{OBA}=\widehat{OCD}\left(AB\text{//}CD\right)\\AB=CD\end{matrix}\right.\Rightarrow\Delta OAB=\Delta OCD\left(g.c.g\right)\\ \Rightarrow OA=OD;OB=OC\)
TG
2
MN
17 tháng 2 2021
Đơn thức là biểu thức đại số chỉ gồm một số, hoặc một biến, hoặc một tích giữa các số và các biến.
=> A
6 tháng 11 2021
d: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{2x+5y}{2\cdot5+5\cdot3}=\dfrac{100}{25}=4\)
Do đó: x=20; y=12
11 tháng 9 2021
a: \(\left|2x-27\right|^{2007}+\left(3y+10\right)^{2008}\ge0\forall x,y\)
Dấu '=' xảy ra khi \(\left(x,y\right)=\left(\dfrac{27}{2};-\dfrac{10}{3}\right)\)
b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4}=\dfrac{x-1-2y+4+3z-9}{2-2\cdot3+3\cdot4}=\dfrac{-10-6}{8}=-2\)
Do đó: \(\left\{{}\begin{matrix}x-1=-4\\y-2=-6\\z-3=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-4\\z=-5\end{matrix}\right.\)
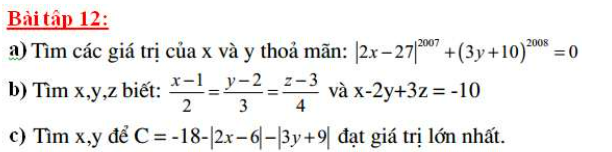
\(\frac{81^{20}.25^{55}}{125^{36}.9^{40}}=\frac{3^{80}.5^{110}}{5^{108}.3^{80}}=\frac{5^{110}}{5^{108}}=5^2=25\)