
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bữa sau bạn nhớ giải thích nữa nha chớ mình không biết tại sao ra đáp án đó đâu

\(x\left(x-y\right)+2\left(y-x\right)=x\left(x-y\right)-2\left(x-y\right)=\left(x-y\right)\left(x-2\right)\)
\(=x\left(x-y\right)-2\left(x-y\right)=\left(x-2\right)\left(x-y\right)\)

\(P=\left(\dfrac{x^2+1}{x^2-9}-\dfrac{x}{x+3}+\dfrac{5}{3-x}\right):\left(\dfrac{2x+10}{x+3}-1\right)\)
\(=\left(\dfrac{x^2+1}{\left(x-3\right)\left(x+3\right)}-\dfrac{x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}-\dfrac{5\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{2x+10}{x+3}-\dfrac{x+3}{x+3}\right)\)
\(=\left(\dfrac{x^2+1-x^2+3x-5x-15}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{2x+10-x-3}{x+3}\right)\)
\(=\left(\dfrac{-2x-14}{\left(x-3\right)\left(x+3\right)}\right):\left(\dfrac{x+7}{x+3}\right)\)
\(=\dfrac{-2\left(x+7\right)}{\left(x-3\right)\left(x+3\right)}.\dfrac{x+3}{x+7}\)
\(=\dfrac{-2}{x-3}\)
đk : x khác -3 ; 3 ; -7
\(P=\left(\dfrac{x^2+1+x\left(x-3\right)+5x+15}{x^2-9}\right):\left(\dfrac{2x+10-x-3}{x+3}\right)\)
\(=\dfrac{2x^2+1+2x+15}{x^2-9}:\dfrac{x+7}{x+3}=\dfrac{2x^2+2x+16}{\left(x-3\right)\left(x+7\right)}\)

6, \(\Rightarrow-2\left(x-3\right)-8=5\left(x+2\right)\Leftrightarrow-2x-2=5x+10\)
\(\Leftrightarrow7x=-12\Leftrightarrow x=-\dfrac{12}{7}\)
7, \(\Rightarrow6\left(2x+1\right)-5\left(x+6\right)=5-4x\Leftrightarrow7x-24=5-4x\)
\(\Leftrightarrow11x=29\Leftrightarrow x=\dfrac{29}{11}\)
8, \(\Rightarrow35-15x-10-2x=10\Leftrightarrow25-17x=10\Leftrightarrow x=\dfrac{15}{17}\)
6: \(\Leftrightarrow-2\left(x-3\right)-8=5x+10\)
=>5x+10=-2x+6-8
=>5x+10=-2x-2
=>7x=-12
hay x=-12/7
7: \(\Leftrightarrow6\left(2x+1\right)-5\left(x+6\right)=5-4x\)
=>12x+6-5x-30-5+4x=0
=>11x-29=0
hay x=29/11
8: \(\Leftrightarrow5\left(7-3x\right)-2\left(x+5\right)=10\)
=>35-15x-2x-10=10
=>-17x=-15
hay x=15/17


Ta có \(x.\left(x^2+x+1\right)-x^2.\left(1+x\right)-x-7\)
\(=x^3+x^2+x-x^2-x^3-x-7\)
\(=\left(x^3-x^3\right)-\left(x^2-x^2\right)-\left(x-x\right)-7\)
\(=-7\)
Do đó giá trị của biểu thức không phụ thuộc vào biến
Vậy...

ta có \(B=x^3+y^3+3xy\)
\(\Rightarrow B=\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\)
\(=3\left(x^2-xy+y^2\right)+3xy\)
\(=3x^2-3xy+3y^2+3xy\)
\(3x^2+3y^2\)


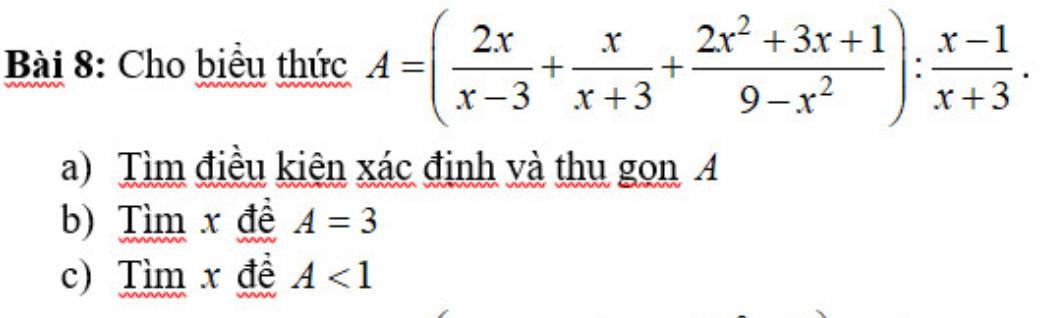 giúp mik câu này thật nhanh nha
giúp mik câu này thật nhanh nha
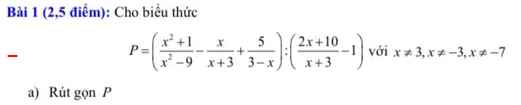
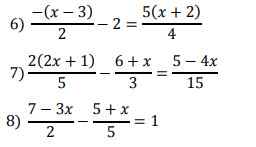
a) Để A xác định thì: \(\left\{{}\begin{matrix}x-3\ne0\\x+3\ne0\\9-x^2\ne0\\\dfrac{x-1}{x+3}\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ne\pm3\\x\ne1\end{matrix}\right.\)
Với \(x\ne\pm3;x\ne1\), ta có:
\(A=\left(\dfrac{2x}{x-3}+\dfrac{x}{x+3}+\dfrac{2x^2+3x+1}{9-x^2}\right):\dfrac{x-1}{x+3}\)
\(=\left[\dfrac{2x\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}+\dfrac{x\left(x-3\right)}{\left(x-3\right)\left(x+3\right)}-\dfrac{2x^2+3x+1}{\left(x-3\right)\left(x+3\right)}\right]\cdot\dfrac{x+3}{x-1}\)
\(=\dfrac{2x^2+6x+x^2-3x-2x^2-3x-1}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x+3}{x-1}\)
\(=\dfrac{x^2-1}{x-3}\cdot\dfrac{1}{x-1}\)
\(=\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x-3\right)\left(x-1\right)}=\dfrac{x+1}{x-3}\)
Vậy \(A=\dfrac{x+1}{x-3}\) với \(x\ne\pm3;x\ne1\).
b) Với \(x\ne\pm3;x\ne1\):
Để \(A=3\) thì \(\dfrac{x+1}{x-3}=3\)
\(\Rightarrow x+1=3\left(x-3\right)\)
\(\Leftrightarrow x+1=3x-9\)
\(\Leftrightarrow x-3x=-9-1\)
\(\Leftrightarrow-2x=-10\Leftrightarrow x=5\) (tm ĐKXĐ)
Vậy \(A=3\) tại \(x=5\).
c) Để \(A< 1\) thì \(\dfrac{x+1}{x-3}< 1\)
\(\Leftrightarrow\dfrac{x+1}{x-3}-1< 0\)
\(\Leftrightarrow\dfrac{x+1-\left(x-3\right)}{x-3}< 0\)
\(\Leftrightarrow\dfrac{4}{x-3}< 0\)
\(\Rightarrow x-3< 0\) (vì \(4>0\))
\(\Leftrightarrow x< 3\)
Kết hợp với ĐKXĐ của \(x\), ta được: \(x< 3;x\ne-3;x\ne1\)
Vậy \(A< 1\) khi \(x< 3;x\ne-3;x\ne1\).
\(\text{#}Toru\)