Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

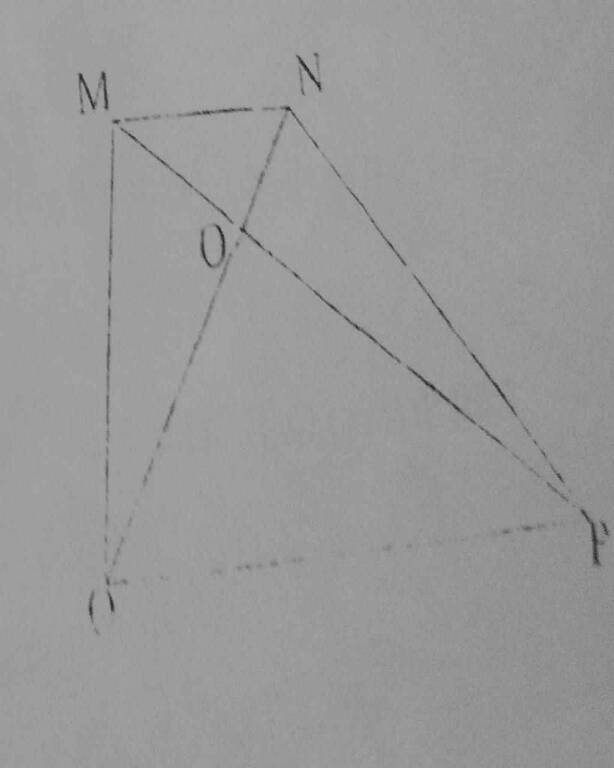
cho hình thang ABCD có diện tích là 90m vuông , đáy bé CB=1/4AD . hai đường chéo AC VÀ BD cắt nhau tại O
a, tính diện tích tam giác BCD
gọi h là chiều cao của hình thang ABCD
\(s_{ABCD}=\frac{1}{2}\left(AD+BC\right)\cdot h\)
\(s_{ABCD}=\frac{1}{2}\left(4.BC+BC\right)\cdot h\)
\(s_{ABCD}=\frac{5}{2}\left(BC\right)\cdot h\)
Mặt khác: \(s_{BCD}=\frac{1}{2}\left(BC\right)\cdot h\)
\(\Rightarrow s_{BCD}=\frac{1}{5}S_{ABCD}\)
\(\Rightarrow s_{BCD}=\frac{90}{5}=18m^2\)
b, so sánh diện tích tam giác AOB và tam giác COD
\(S_{\Delta ABC}=S_{\Delta DCB}\)Vì cùng đáy CB và chiều cao h.
\(\Leftrightarrow S_{\Delta ABO}+S_{\Delta BOC}=S_{\Delta DCO}+S_{\Delta BOC}\)
\(\Leftrightarrow S_{\Delta ABO}=S_{\Delta DCO}\)
A B C D O