
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.

Bài 3:
Diện tích là:
\(15\cdot6=90\left(m^2\right)\)
Bài 3:
Gọi cd,cr lần lượt là a,b(m;a,b>0)
Áp dụng tc dtsbn:
\(\dfrac{b}{a}=\dfrac{2}{5}\Rightarrow\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{2a+2b}{10+4}=\dfrac{42}{14}=3\\ \Rightarrow\left\{{}\begin{matrix}a=15\\b=6\end{matrix}\right.\\ \Rightarrow S_{hcn}=ab=90\left(m^2\right)\)
Bài 4:
Gọi cd,cr lân lượt là a,b(m;a,b>0)
Đặt \(\dfrac{a}{4}=\dfrac{b}{3}=k\Rightarrow a=4k;b=3k\)
\(ab=300\left(m^2\right)\\ \Rightarrow12k^2=300\\ \Rightarrow k^2=25\Rightarrow k=5\left(k>0\right)\\ \Rightarrow\left\{{}\begin{matrix}a=20\\b=15\end{matrix}\right.\)
Vậy ...
Bài 5:
Gọi số hs 7A,7B,7C,7D ll là a,b,c,d(hs;a,b,c,d∈N*)
Áp dụng tc dtsbn:
\(\dfrac{a}{11}=\dfrac{b}{12}=\dfrac{c}{13}=\dfrac{d}{14}=\dfrac{2b-a}{24-11}=\dfrac{39}{13}=3\\ \Rightarrow\left\{{}\begin{matrix}a=33\\b=36\\c=39\\d=42\end{matrix}\right.\)
Vậy ...


Bài 77:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{9}=\dfrac{y-x}{9-8}=5\)
Do đó: x=40; y=45

a: AD+DB=AB
AE+EC=AC
mà DB=EC và AB=AC
nên AD=AE
Xét ΔABC có AD/AB=AE/AC
nên DE//BC
b: Xét ΔABE và ΔACD có
AB=AC
góc A chung
AE=AD
=>ΔABE=ΔACD
c: Xét ΔIDB và ΔIEC có
góc IDB=góc IEC
DB=EC
góc IBD=góc ICE
=>ΔIDB=ΔIEC
d: Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
=>ΔAIB=ΔAIC
=>góc BAI=góc CAI
=>AI là phângíac của góc BAC
e: AB=AC
IB=IC
=>AI là trung trực của BC
=>AI vuông góc BC

\(\left(3+\frac{1}{3}\right):4,8=0,5:7\)
\(\left(3+\frac{1}{3}\right):4,8=\frac{1}{14}\)
\(3+\frac{1}{3}=\frac{1}{14}.4,8=\frac{12}{35}\)
=> Đề bài bị lỗi hở bạn ???

Câu 4:
Ta có: \(\left|x+2\right|\ge0\forall x\)
\(\left|2y+3\right|\ge0\forall y\)
Do đó: \(\left|x+2\right|+\left|2y+3\right|\ge0\forall x,y\)
Dấu '='xảy ra khi x=-2 và \(y=-\dfrac{3}{2}\)

Ta có: x=2017 suy ra: x+1=2018
Thay x+1=2018 vào biểu thức A,ta có:
\(x^{20}-x+1.x^{19}-x+1.x^{18}-...-x+1.x-1=x^{20}-x^{20}-x^{19}+x^{19}+...+x-1\)
Suy ra: x-1=2017-1=2016
Vậy x=2016

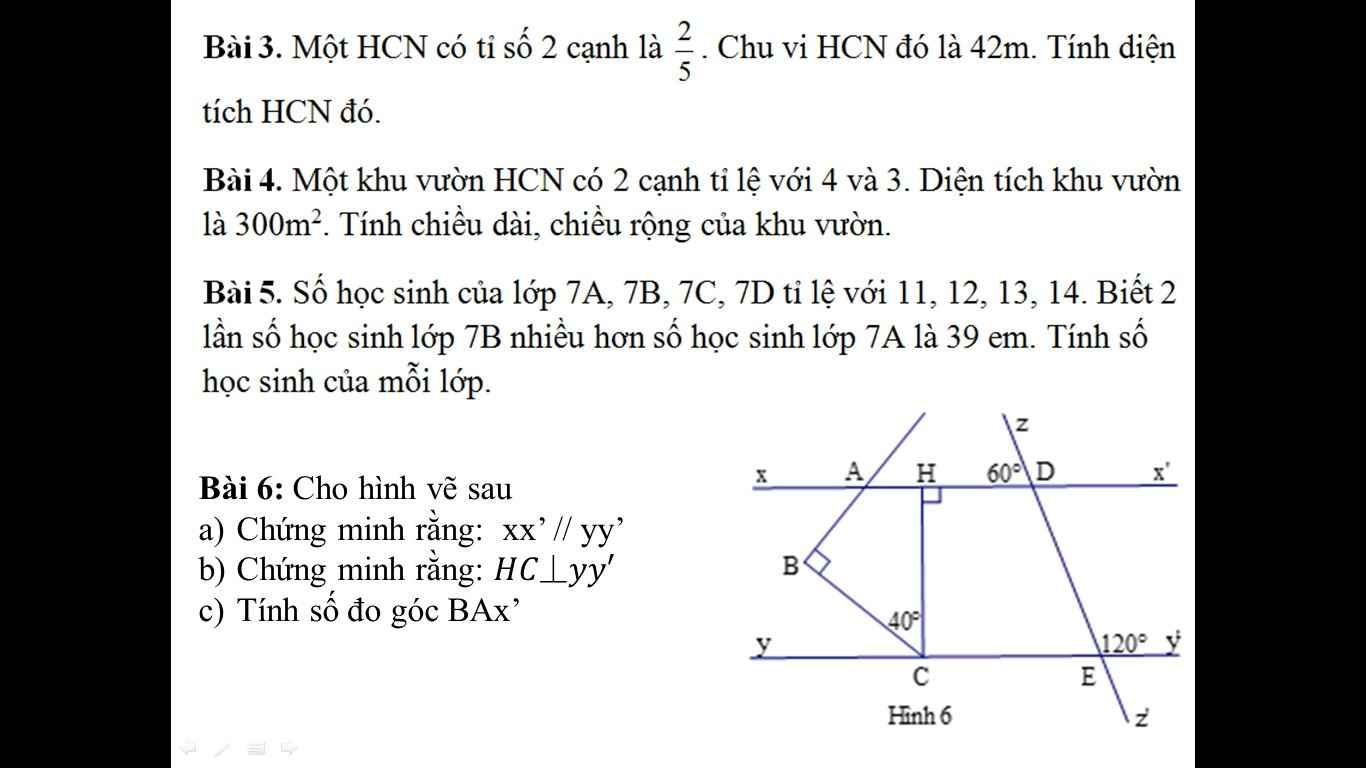

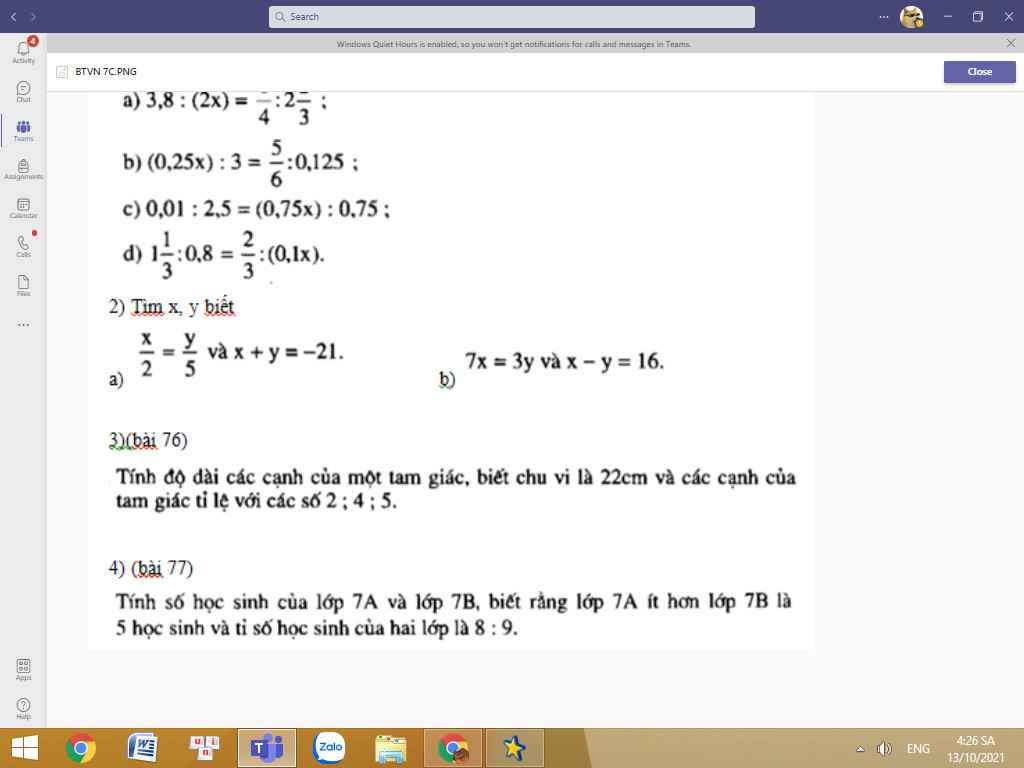 ai giúp em làm câu này vs em đang cần gấp ạ
ai giúp em làm câu này vs em đang cần gấp ạ

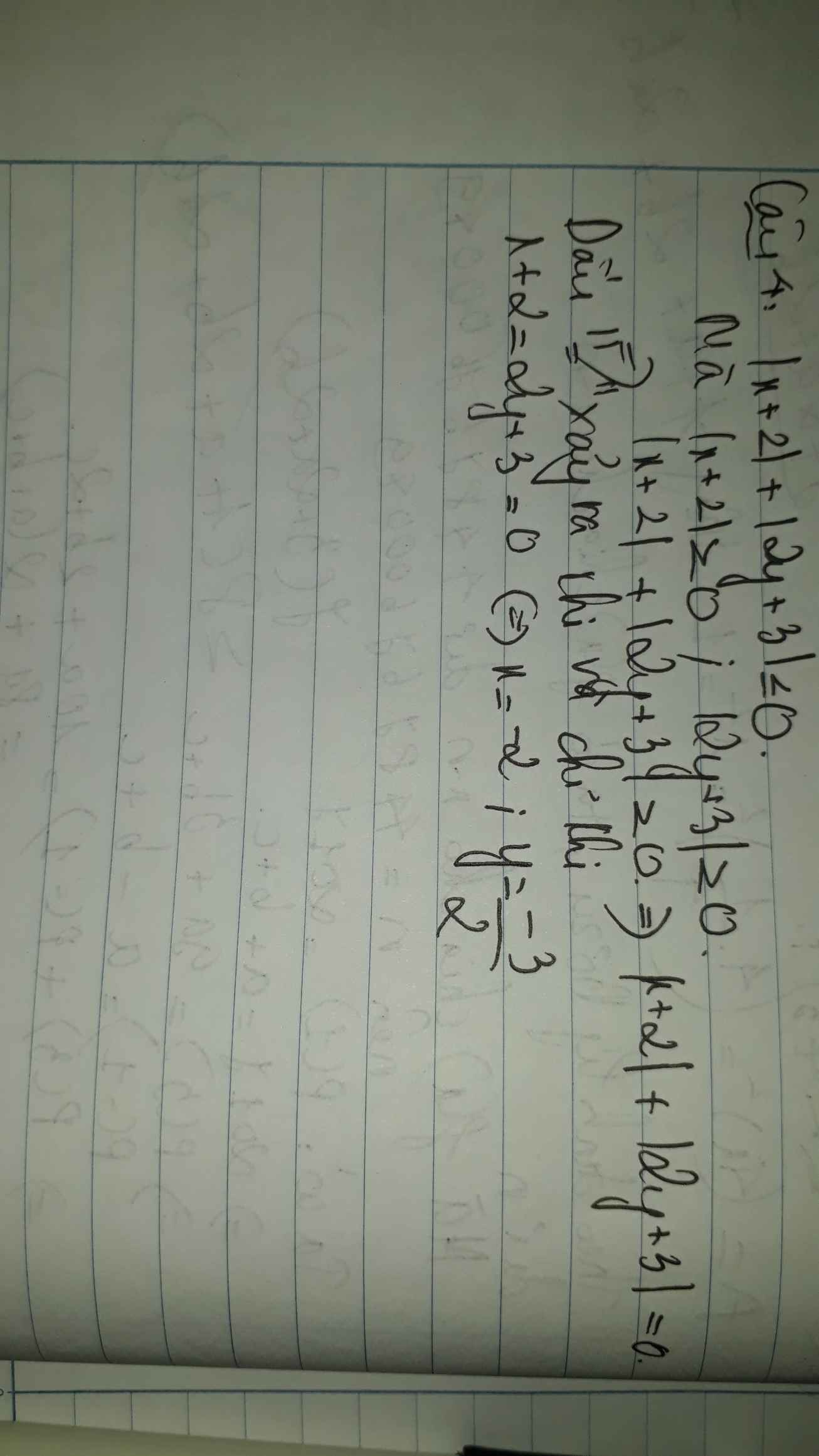
mình mới hoc lớp 6 thôi khó quá
a, \(A=2x^2-2\ge-2\)
Dấu ''='' xảy ra khi x = 0
Vậy GTNN của A là -2 khi x = 0
b, \(B=\left|x+\frac{1}{3}\right|-\frac{1}{6}\ge-\frac{1}{6}\)
Dấu ''='' xảy ra khi x = -1/3
Vậy GTNN của B là -1/6 khi x = -1/3
c, \(C=\left|x\right|+\frac{2017}{2018}\ge\frac{2017}{2018}\)
Dấu ''='' xảy ra khi x = 0
Vậy GTNN của C là 2017/2018 khi x = 0
d, \(D=-\left(x+1\right)^2+3\le3\)
Dấu ''='' xảy ra khi x = -1
Vậy GTLN của D là 3 khi x = -1
e, \(E=-\left|0,1+x\right|-1,9\le-1,9\)
Dấu ''='' xảy ra khi x = -0,1
Vậy GTLN của E là -1,9 khi x = -0,1
f, Ta có : \(\left|x\right|+2017\ge2017\)
\(\Rightarrow F\le\frac{1}{2017}\)
Dấu ''='' xảy ra khi x = 0
Vậy GTLN của F là 1/2017 khi x = 0