
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
b) Xét ΔABC có AB<AC<BC(3cm<4cm<5cm)
mà góc đối diện với cạnh AB là \(\widehat{ACB}\)
và góc đối diện với cạnh AC là \(\widehat{ABC}\)
và góc đối diện với cạnh BC là \(\widehat{BAC}\)
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
Xét ΔABC có
HB là hình chiếu của AB trên BC
HC là hình chiếu của AC trên BC
AB<AC
Do đó: HB<HC
c) Xét ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD(gt)
Do đó: ΔCAB=ΔCAD(hai cạnh góc vuông)
Suy ra: CB=CD(hai cạnh tương ứng)
Xét ΔCBD có CB=CD(cmt)
nên ΔCBD cân tại C(Định nghĩa tam giác cân)

Bài 5:
f(x) có 1 nghiệm x - 2
=> f (2) = 0
\(\Rightarrow a.2^2-a.2+2=0\)
\(\Rightarrow4a-2a+2=0\)
=> 2a + 2 = 0
=> 2a = -2
=> a = -1
Vậy:....
P/s: Mỗi lần chỉ đc đăng 1 câu hỏi thôi! Bạn vui lòng đăng bài hình trên câu hỏi khác nhé!
a)Ta có △MIP cân tại M nên ˆMNI=ˆMPIMNI^=MPI^
Xét △MIN và △MIP có:
ˆNMI=ˆPMINMI^=PMI^
MI : cạnh chung
ˆMNI=ˆMPIMNI^=MPI^
Nên △MIN = △MIP (c.g.c)
b)Gọi O là giao điểm của EF và MI
Vì △MNP là tam giác cân và MI là đường phân giác của △MIP
Suy ra MI đồng thời là đường cao của △MNP
Nên ˆMOE=ˆMOF=90oMOE^=MOF^=90o
Xét △MOE vuông tại O và △MOF vuông tại O có:
OM : cạnh chung
ˆEMO=ˆFMOEMO^=FMO^(vì MI là đường phân giác của △MIP và O∈∈MI)
Suy ra △MOE = △MOF (cạnh góc vuông – góc nhọn kề)
Nên ME = MF
Vậy △MEF cân
tham khảo

a: Xét ΔDBH có
BA là đường cao
BA là đường trung tuyến
Do đó: ΔDBH cân tại B
b: AC=10cm
=>AB=5cm
\(BC=\sqrt{5^2+10^2}=5\sqrt{5}\left(cm\right)\)

-Hình vẽ:
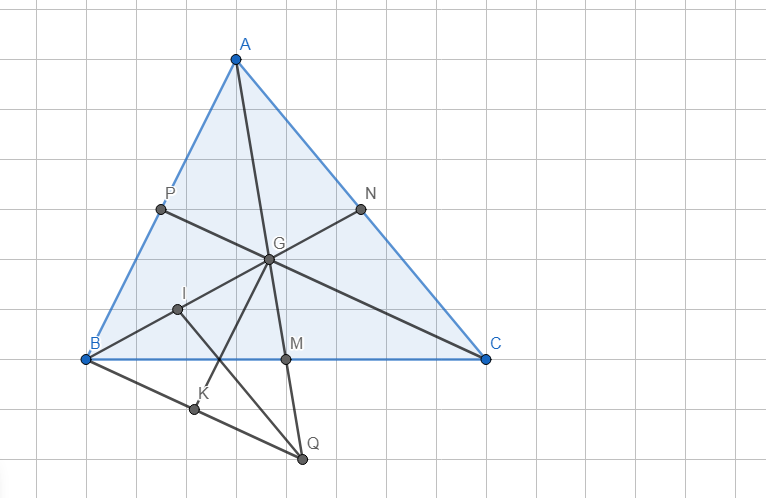
a) -Xét △ABC có:
AM là trung tuyến (gt).
BN là trung tuyến (gt).
G là giao của AM và BN (gt)
=>G là trọng tâm của △ABC.
=>\(BG=\dfrac{2}{3}BN\)(1) (t/c trọng tâm).
\(CG=\dfrac{2}{3}CP\) (2) (t/c trọng tâm).
\(AG=\dfrac{2}{3}AM=2GM\) (t/c trọng tâm).
Mà \(GQ=2GM\) (M là trung điểm GQ).
=>\(GQ=AG=\dfrac{2}{3}AM\) (3).
-Từ (1),(2),(3) suy ra: Độ dài các đường trung tuyến của △BGQ bằng \(\dfrac{1}{2}\) độ dài các cạnh tương ứng của △ABC.
b) -Xét △BMQ và △CMG ta có:
\(BM=CM\) (M là trung điểm của BC).
\(\widehat{BMQ}=\widehat{CMG}\) (đối đỉnh).
\(MQ=MG\) (M là trung điểm GQ)
=>△BMQ = △CMG (c-g-c).
=>\(BQ=CG\) (2 cạnh tương ứng).
-Ta có: \(BC< BG+CG\) (bất đẳng thức trong △BGC).
=>\(BC< BG+BQ\) (\(BQ=CG\))
=>\(\dfrac{1}{2}BC< \dfrac{1}{2}\left(BG+BQ\right)\)
Mà \(BM=\dfrac{1}{2}BC\) (M là trung điểm BC).
=>\(BM< \dfrac{1}{2}\left(BG+BQ\right)\).
c) -Ta có: \(BG=2GN\) (G là trọng tâm của △ABC).
Mà \(BG=2IG\) (I là trung điểm của BG).
=>\(GN=IG\).
-Xét △IQG và △NAG có:
\(IG=NG\) (cmt).
\(\widehat{IGQ}=\widehat{NQA}\) (đối đỉnh).
\(QG=AG\) (cmt).
=>△IQG = △NAG (c-g-c).
=>\(IQ=AN\) (2 cạnh tương ứng) mà \(AN=\dfrac{1}{2}AC\) (N là trung điểm AC).
=>\(IQ=\dfrac{1}{2}AC\) (4).
-Ta có: \(CG=2GP\) (G là trọng tâm của △ABC).
Mà \(BQ=2BK\) (K là trung điểm BQ) và \(BQ=CG\) (cmt).
=>\(GP=BK\).
-Ta có: \(\widehat{BQM}=\widehat{CGM}\)(△BMQ = △CMG).
Mà 2 góc này ở vị trí so le trong.
=>BQ//CG.
-Xét △GBK và △BGP có:
\(BK=GP\left(cmt\right)\)
\(\widehat{KBG}=\widehat{PGB}\) (BK//PQ và so le trong).
\(BG\) là cạnh chung.
=>△GBK = △BGP (c-g-c).
=>\(GK=BP\) (2 cạnh tương ứng) mà \(BP=\dfrac{1}{2}AB\) (P là trung điểm AB).
=>\(GK=\dfrac{1}{2}AB\) (2).
-Từ (1) và (2) và \(BM=\dfrac{1}{2}BC\) (M là trung điểm BC) suy ra:
Độ dài các đường trung tuyến của △BGP bằng \(\dfrac{1}{2}\) độ dài các cạnh tương ứng của △ABC.

a) Ta có: \(P\left(x\right)=7x^3+3x^4-x^2+5x^2-6x^3-2x^4+2017-x^3\)
\(=x^4+4x^2+2017\)
b) Bậc của P(x) là 4
c) Các hệ số của P(x) là 1;4;2017
Hệ số cao nhất là 4
Hệ số tự do là 2017
d) \(P\left(0\right)=0^4+4\cdot0^2+2017=2017\)
\(P\left(1\right)=1^4+4\cdot1^2+2017=1+4+2017=2022\)
\(P\left(-1\right)=\left(-1\right)^4+4\cdot\left(-1\right)^2+2017=1+4+2017=2022\)
e) \(P\left(-a\right)=\left(-a\right)^4+4\cdot\left(-a\right)^2+2017=a^4+4a^2+2017\)
\(P\left(a\right)=a^4+4a^2+2017\)
Do đó: P(-a)=P(a)

`# \text {Kaizu DN}`
`a)`
`(3x + 6) + (7x - 14) = 0?`
\(\Rightarrow3x+6+7x-14=0\\ \Rightarrow\left(3x+7x\right)+\left(6-14\right)=0\\ \Rightarrow10x-8=0\\ \Rightarrow10x=8\Rightarrow x=\dfrac{8}{10}\\ \Rightarrow x=\dfrac{4}{5}\)
Vậy, \(x=\dfrac{4}{5}\)
`b)`
`17y + 35 + 4x + 17 = 42`
\(\Rightarrow\left(17y+17\right)+\left(35+4x\right)=42\\ \Rightarrow17\left(y+1\right)+\left(35+4x\right)=42\)
Bạn xem lại đề ;-;.

GIÚP MIK VS NHA:(((((
CẢM ƠN RẤT NHIỀU
MN XONG CÂU NÀO THÌ CỨ GỬI LUÔN CHO MIK CÂU ĐÓ NHA;-;
MIK CÒN CHÉP KỊP
:(((((((((((((( NHANHH NHANH GIÚP MIK Ạ
Câu 1:
\(a,\dfrac{x}{4}=\dfrac{y}{7}=\dfrac{x-y}{4-7}=\dfrac{-15}{-3}=5\\ \Rightarrow\left\{{}\begin{matrix}x=20\\y=35\end{matrix}\right.\\ b,\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{x+y}{3+5}=\dfrac{-32}{8}=-4\\ \Rightarrow\left\{{}\begin{matrix}x=-12\\y=-20\end{matrix}\right.\\ c,\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}=\dfrac{x+y+z}{2+3+5}=\dfrac{-90}{10}=-9\\ \Rightarrow\left\{{}\begin{matrix}x=-18\\y=-27\\z=-45\end{matrix}\right.\\ d,\dfrac{x}{4}=\dfrac{y}{2}=\dfrac{z}{7}=\dfrac{2x-4y+3z}{8-8+21}=\dfrac{42}{21}=2\\ \Rightarrow\left\{{}\begin{matrix}x=8\\y=4\\z=14\end{matrix}\right.\)
\(e,\dfrac{x}{5}=\dfrac{y}{6}=\dfrac{z}{7}=\dfrac{z-x}{7-5}=\dfrac{30}{2}=15\\ \Rightarrow\left\{{}\begin{matrix}x=75\\y=90\\z=105\end{matrix}\right.\\ f,\Rightarrow\dfrac{x}{3}=\dfrac{y}{5};\dfrac{x}{4}=\dfrac{z}{3}\Rightarrow\dfrac{x}{12}=\dfrac{y}{20}=\dfrac{z}{9}=\dfrac{x-y-z}{12-20-9}=\dfrac{-68}{-17}=4\\ \Rightarrow\left\{{}\begin{matrix}x=48\\y=80\\z=36\end{matrix}\right.\\ g,\Rightarrow\dfrac{x}{6}=\dfrac{y}{4}=\dfrac{z}{3}=\dfrac{x+y+z}{6+4+3}=\dfrac{65}{13}=5\\ \Rightarrow\left\{{}\begin{matrix}x=30\\y=20\\z=15\end{matrix}\right.\\ h,\Rightarrow\dfrac{x}{4}=\dfrac{y}{6};\dfrac{y}{5}=\dfrac{z}{8}\Rightarrow\dfrac{x}{20}=\dfrac{y}{30}=\dfrac{z}{48}=\dfrac{5x-3y-3z}{100-90-144}=\dfrac{-536}{-134}=4\\ \Rightarrow\left\{{}\begin{matrix}x=80\\y=120\\z=192\end{matrix}\right.\)


Tiến hành phân bổ bình quân theo tỷ lệ thuận số người mỗi đội, ta có
Số dụng cụ đội 1: 108/(10+12+5) x 10 = 40
Số dụng cụ đội 2: 108/(10+12+5)x12 = 48
Số dụng cụ đội 3: 108/(10+12+5)x5 = 20







a, bằng âm 23/30
b, bằng 19/3