K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
15 tháng 1 2022
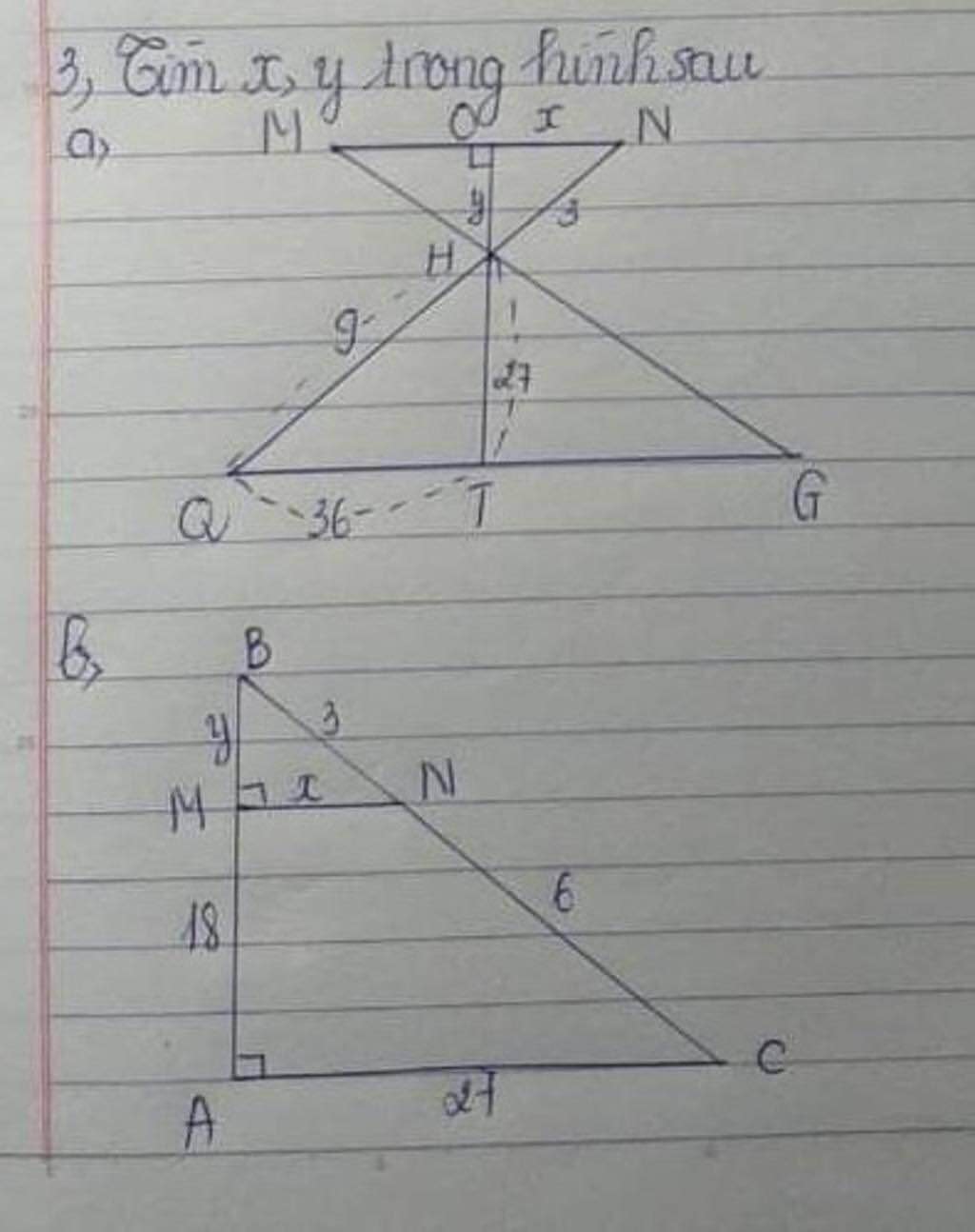
b: Xét ΔABC có MN//AC
nên BM/MA=BN/NC=1/2
=>y=9cm
Xét ΔBAC có MN//AC
nên x/27=3/9=1/3
=>x=9
giúp em với em đang cần giải gấp
7 tháng 2 2022
1: =>7x-4x=8+7
=>3x=15
hay x=5
2: \(\Leftrightarrow3-2x=3x+3-x-2\)
=>3-2x=2x+1
=>-4x=-2
hay x=1/2
3: \(\Leftrightarrow15x+10-4x-1=0\)
=>11x+9=0
hay x=-9/11
4: \(\Leftrightarrow6x-2=x-2\)
hay x=0
5: \(\Leftrightarrow2x+2x=32-7\)
=>4x=25
hay x=25/4
TP
20 tháng 3 2022
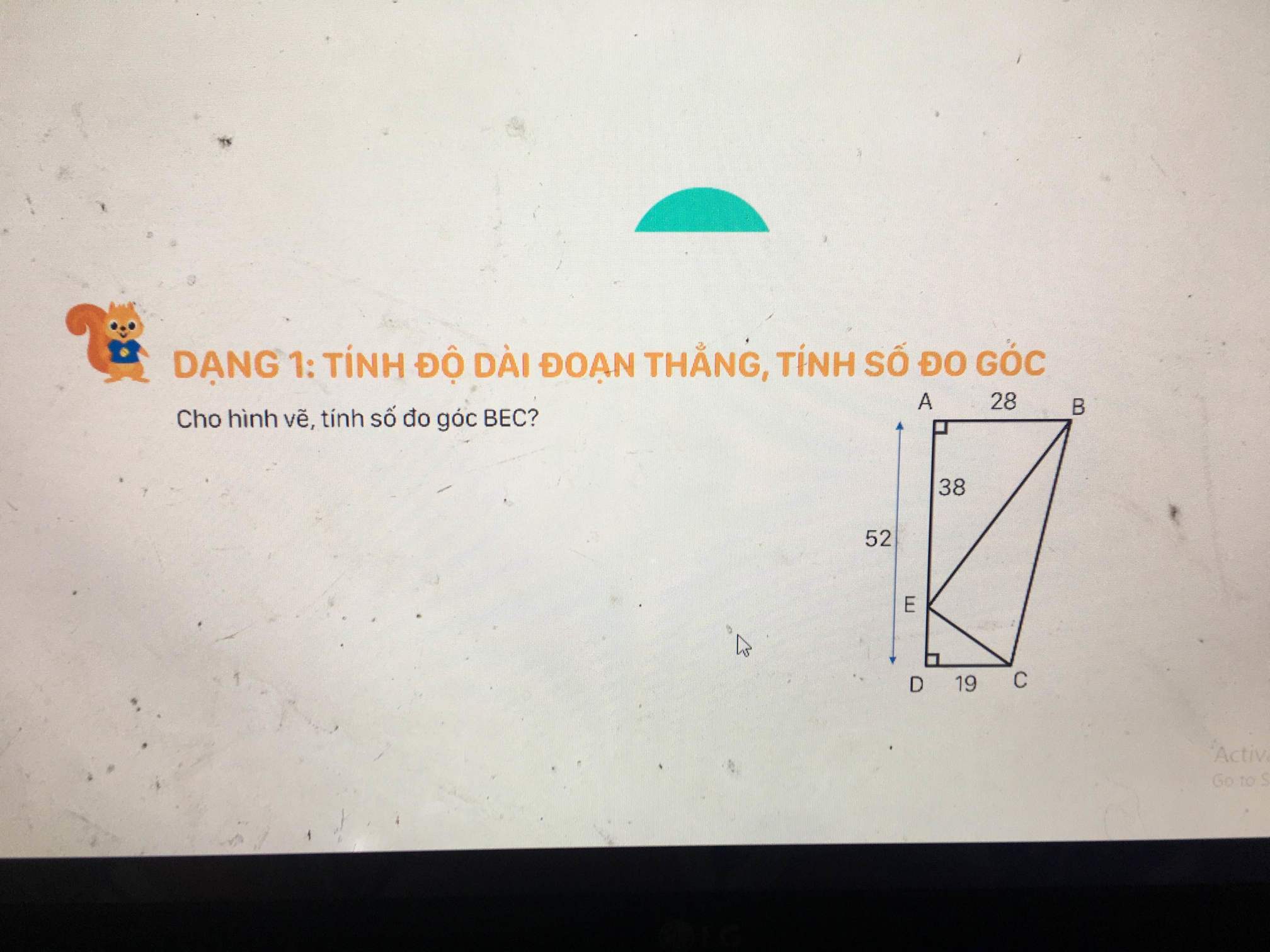
vì be là đường cao của tam giác abc :
=)góc bec = góc bea =90
vì ch là đường cao của tam giác abc (gt)
=) góc bch = góc cha =90
xét tam giác ahc và tam giác aeb ta có
góc ahc =góc aeb( =90)
góc a chung
=) tam giác ahc ~TAM GIÁC EAB(g.g)
b, gọi i là giao điểm của be và ch
xét tam giác hib và tam giác eic ta có
h2 =e2 =90
i1=i2 ( 2gocs đối đỉnh)
=)hib ~eic (g.g)
do mk đang bận nên chỉ giải đc đến đây thôi ạ
29 tháng 12 2021
b: \(\Leftrightarrow\left(x-3\right)\left(x-5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=5\end{matrix}\right.\)
24 tháng 10 2021
\(x^2-x-6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}A=3^4+2\cdot3^3+2\cdot3^2+2\cdot3+1=160\\A=\left(-2\right)^4+2\cdot\left(-2\right)^3+2\cdot\left(-2\right)^2+2\cdot\left(-2\right)+1=5\end{matrix}\right.\)
MM
Mai Minh Tú
VIP
7 tháng 1 2022
9999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999911111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111112222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222222233333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444445555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555555566666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666666777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888101010101010101010010101010100101010101001001010101010100101010101001010101010100101010101010010101010011001