Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
góc CDH+góc CEH=90+90=180 độ
=>CDHE nội tiếp
b: góc AFH+góc AEH=180 độ
=>AFHE nội tiếp
góc FEH=góc BAD
góc DEH=góc FCB
mà góc BAD=góc FCB
nên góc FEH=góc DEH
=>EH là phân giác của góc FED
Xét ΔBFE và ΔDHE có
góc BEF=góc DEH
góc BFE=góc DHE
=>ΔBFE đồng dạng với ΔDHE

a: Xét tứ giác BCEF có
\(\widehat{BFC}=\widehat{BEC}\)
nên BCEF là tứ giác nội tiếp
Xét tứ giác CDHE có
\(\widehat{HDC}+\widehat{HEC}=180^0\)
Do đó: CDHE là tứ giác nội tiếp

a: Xét tứ giác BCEF có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
Do đó: BCEF là tứ giác nội tiếp
Xét tứ giác CDHE có
\(\widehat{CDH}+\widehat{CEH}=180^0\)
Do đó: CDHE là tứ giác nội tiếp
b: \(\widehat{FEB}=\widehat{BAD}\)(vì AFHE là tứ giác nội tiếp)
\(\widehat{BED}=\widehat{FCB}\)(BFEC là tứ giác nội tiếp)
mà \(\widehat{BAD}=\widehat{FCB}\)
nên \(\widehat{FEB}=\widehat{BED}\)
hay EB là tia phân giác góc FED

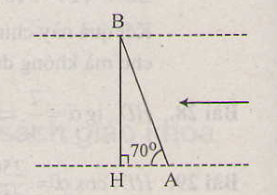
Gọi AB là đoạn đường mà con thuyền đi được trong 6p, BH là chiều rộng của khúc sông
=>ΔBHA vuông tại H
AB=20*1/10=2(km)=2000(m)
Xét ΔBHA vuông tại H có BH=BA*sinA
=>\(BH=2000\cdot sin40\simeq1285,58\left(m\right)\)

góc AEB=góc ADB=90 độ
=>AEDB nội tiếp
góc CDH+góc CEH=180 độ
=>CEHD nội tiếp

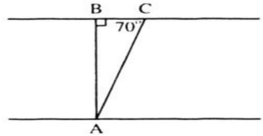
Kí hiệu như hình vẽ, trong đó:
AB là chiều rộng của khúc sông (cũng chính là đường đi của thuyền khi không có nước chảy).
AC là đoạn đường đi của chiếc thuyền (do nước chảy nên thuyền bị lệch).
Theo đề bài: v = 2km/h ; t = 5 phút = 1/12 h
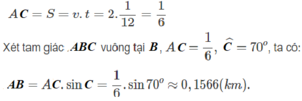
Vậy chiều rộng khúc sông là 0,1566 km = 156,6 m.

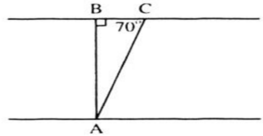
Kí hiệu như hình vẽ, trong đó:
AB là chiều rộng của khúc sông (cũng chính là đường đi của thuyền khi không có nước chảy).
AC là đoạn đường đi của chiếc thuyền (do nước chảy nên thuyền bị lệch).
Theo đề bài: v = 2km/h ; t = 5 phút = 1/12 h
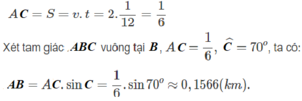
Vậy chiều rộng khúc sông là 0,1566 km = 156,6 m.
Bài 2:
a: Xét tứ giác CDHE có \(\widehat{CDH}+\widehat{CEH}=90^0+90^0=180^0\)
nên CDHE là tứ giác nội tiếp
b: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp
=>\(\widehat{BFE}+\widehat{BCE}=180^0\)
mà \(\widehat{BCE}+\widehat{DHE}=180^0\)
nên \(\widehat{BFE}=\widehat{DHE}\)
Ta có: \(\widehat{BEF}=\widehat{BCF}\)(BFEC nội tiếp)
\(\widehat{BCF}=\widehat{DEH}\)(CDHE nội tiếp)
Do đó: \(\widehat{BEF}=\widehat{DEH}\)
Xét ΔBEF và ΔDEH có
\(\widehat{BEF}=\widehat{DEH}\)
\(\widehat{BFE}=\widehat{DHE}\)
Do đó: ΔBEF~ΔDEH