Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 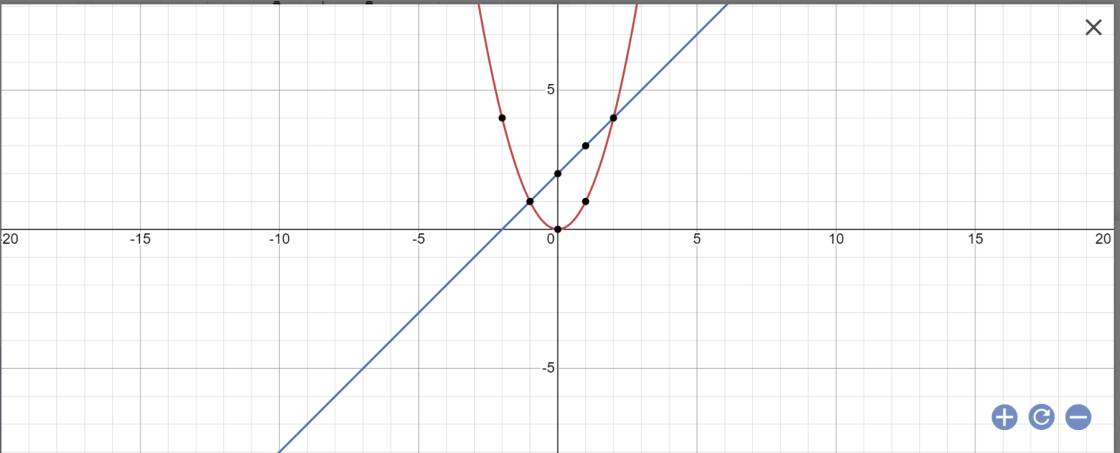
b: PTHĐGĐ là:
x^2-x-2=0
=>(x-2)(x+1)=0
=>x=2 hoặc x=-1
=>y=4 hoặc y=1
c: PTHĐGĐ là:
x^2-2x+m=0
Để (P) cắt (d1) tại hai điểm nằm về hai phía của trục tung thì m<0

pt hoành độ giao điểm của (P) và (d) là \(mx^2=-3x+1\)\(\Leftrightarrow mx^2+3x-1=0\)(*)
pt (*) có \(\Delta=3^2-4.m.\left(-1\right)=4m+9\)
Vậy để (d) cắt (P) tại 2 điểm phân biệt thì \(\Delta=4m+9>0\Leftrightarrow m>-\frac{9}{4}\Leftrightarrow\hept{\begin{cases}m>-\frac{9}{4}\\m\ne0\end{cases}}\)
Khi đó áp dụng định lí Vi-ét, ta có \(x_1x_2=-\frac{1}{m}\)
A và B nằm cùng phía với trục tung \(\Rightarrow x_1,x_2\)cùng dấu \(\Rightarrow x_1x_2>0\)\(\Rightarrow-\frac{1}{m}>0\)\(\Leftrightarrow\frac{1}{m}< 0\)\(\Leftrightarrow m< 0\)
Vậy để (d) cắt (P) tại 2 điểm phân biệt thỏa mãn yêu cầu đề bài thì \(-\frac{9}{4}< m< 0\)

Phương trình hoành độ giao điểm (d) và (P) là:
\(x^2=-\left(m+2\right)x-m-1\)
\(\Leftrightarrow x^2+\left(m+2\right)x+m+1=0\)(1)
Để (d) cắt (P) tại hai điểm phân biệt thì phương trình (1) có hai nghiêm phân biệt. Khi đó:
\(\Delta>0\Leftrightarrow\left(m+2\right)^2-4\left(m+1\right)=m^2>0\Leftrightarrow m\ne0\)
Với \(m\ne0\)phương trình (1) có hai nghiệm phân biệt \(x_1,x_2;x_1>x_2\).
Theo định lí Viete:
\(\hept{\begin{cases}x_1+x_2=-m-2\\x_1x_2=m+1\end{cases}}\)
Do hai điểm nằm khác phía với trục tung nên \(x_1,x_2\)trái dấu nên \(m+1< 0\Leftrightarrow m< -1\).
\(\sqrt{y_1}+\sqrt{y_2}=\sqrt{x_1^2}+\sqrt{x_2^2}=\left|x_1\right|+\left|x_2\right|=x_1-x_2=2\)(do hai điểm nằm khác phía với trục tung)
\(\hept{\begin{cases}x_1+x_2=-m-2\\x_1-x_2=2\end{cases}}\Leftrightarrow\hept{\begin{cases}x_1=\frac{-m}{2}\\x_2=\frac{-m-4}{2}\end{cases}}\)
\(x_1x_2=-\frac{m}{2}\left(\frac{-m-4}{2}\right)=\frac{m\left(m+4\right)}{4}=m+1\Leftrightarrow m=\pm2\).
Vậy \(m=-2\).

cj ơi, nó có trog câu hỏi tương tự rồi ạ, cô Loan giải rồi ạ!!^^
b) Phương trình hoành đọ giao điểm của (P) và (d) là:
x2 = mx + 1
<=> x2 - mx - 1 = 0
$\Delta$Δ = (-m)2 + 4 = m2 + 4 > 0 với mọi m
=> Pt có 2 nghiệm pb với mọi m
=> (P) luôn cắt (d) tại 2 điểm phân biệt A;B
Theo Vi - et ta có: xAxB = -1 < 0
=> xA ; xB trái dấu => A; B nằm khác phía so với trục tung




Chắc đề là \(y=x^2\) chứ ko phải \(y=2^2\)
Phương trình hoành độ giao điểm: \(x^2-3x-m=0\) (1)
\(\Delta=9+4m>0\Rightarrow m>-\frac{9}{4}\)
Để d cắt (P) tại 2 điểm nằm về 2 phía trục tung \(\Leftrightarrow\left(1\right)\) có 2 nghiệm phân biệt trái dấu
\(\Leftrightarrow ac< 0\Leftrightarrow-m< 0\Rightarrow m>0\)