
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\left(x^2-2x+3\right)\left(\frac{1}{2x}-5\right)\)
\(=\frac{x^2}{2x}-5x^2-\frac{2x}{2x}+10x+\frac{3}{2x}-15\)
\(=\frac{x^2}{2x}-5x^2-16+10x+\frac{3}{2x}\)
\(=-5x^2+\frac{x^2}{2x}+\frac{20x^2}{2x}+\frac{3}{2x}-16\)
\(=-5x^2+\frac{x^2+20x+3}{2x}-16\)
học tốt
(x^2-2x+3)(1/2x-5)=1/2x^3-5x^2-x^2+10x+3/2x-15=1/2x^3-6x^2+11,5x-15


\(a,=x^2+x+4x+4=\left(x+1\right)\left(x+4\right)\\ b,=x^2+2x-3x-6=\left(x-3\right)\left(x+2\right)\\ c,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ d,=3\left(x^2-2x+5x-10\right)=3\left(x-2\right)\left(x+5\right)\\ e,=-3x^2+6x-x+2=\left(x-2\right)\left(1-3x\right)\\ f,=x^2-x-6x+6=\left(x-1\right)\left(x-6\right)\\ h,=4\left(x^2-3x-6x+18\right)=4\left(x-3\right)\left(x-6\right)\\ i,=3\left(3x^2-3x-8x+5\right)=3\left(x-1\right)\left(3x-8\right)\\ k,=-\left(2x^2+x+4x+2\right)=-\left(2x+1\right)\left(x+2\right)\\ l,=x^2-2xy-5xy+10y^2=\left(x-2y\right)\left(x-5y\right)\\ m,=x^2-xy-2xy+2y^2=\left(x-y\right)\left(x-2y\right)\\ n,=x^2+xy-3xy-3y^2=\left(x+y\right)\left(x-3y\right)\)

a) \(\dfrac{A}{x-3}=\dfrac{y-x}{3-x}\left(Đk:x\ne3\right)\)
\(A=\dfrac{\left(x-3\right)\left(y-x\right)}{3-x}=x-y\)
b) \(\dfrac{5x}{x+1}=\dfrac{Ax\left(x-1\right)}{\left(1-x\right)\left(x+1\right)}\left(Đk:x\ne\pm1\right)\)
\(A=\dfrac{5x\left(1-x\right)\left(x+1\right)}{x\left(x-1\right)\left(x+1\right)}=-5\)
c) \(\dfrac{4x^2-5x+1}{A}=\dfrac{4x-1}{x+3}\left(Đk:x\ne-3;A\ne0\right)\)
\(A=\dfrac{\left(4x^2-5x+1\right)\left(x+3\right)}{4x-1}=\dfrac{\left(x-1\right)\left(4x-1\right)\left(x+3\right)}{4x-1}\)
\(=\left(x-1\right)\left(x+3\right)=x^2+2x-3\)

Ta có: ΔABC∼ΔDEF
nên DE/AB=EF/BC=DF/AC
=>9/6=EF/10=DF/14
=>EF/10=DF/14=3/2
=>EF=15cm; DF=21cm


3) \(\sqrt{\left(x-2\right)\left(x+1\right)}\) thì (x-2)(x+1)>0
=> x2 -x-2>0
=> x2 - x - \(\dfrac{1}{2}\)- \(\dfrac{3}{2}\)>0
= (x+\(\dfrac{1}{4}\))2 - 3/2 >0
=> x+ 1/4>3/2
=> x>5/4
4) Có x đâu mà tìm bạn??


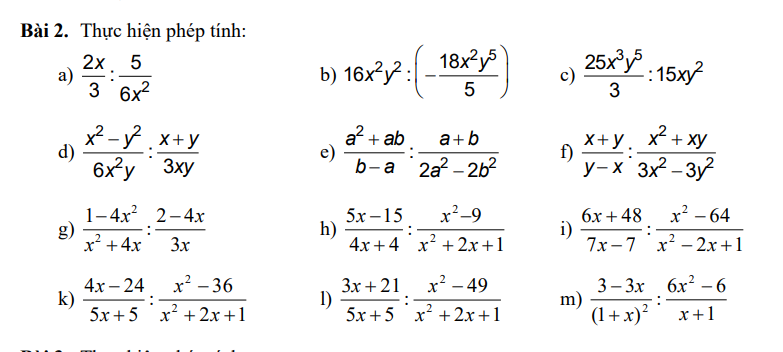

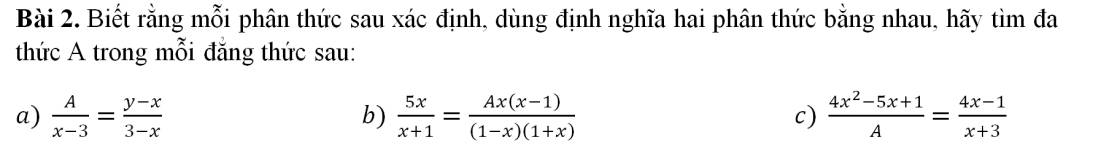 giúp em bài này với ạ ! Em cảm ơn ạ
giúp em bài này với ạ ! Em cảm ơn ạ  Giúp mình làm bài này với ạ
Giúp mình làm bài này với ạ



mấy chỗ này rút gọn đi thôi
a) \(\frac{-4xy^2}{2x^4y}=\frac{2y}{-x^3}\)
Biến đổi vế trái ta có:
\(\frac{-4xy^2}{2x^4y}=\frac{-2y}{x^3}=\frac{2y}{-x^3}\)
=> 2y/-x^3=2y/-x^3
Nên \(\frac{-4xy^2}{2x^4y}=\frac{2y}{-x^3}\) ( đpcm)
b) \(\frac{m^2-2mn+n^2}{m^2-n^2}=\frac{m-n}{m+n}\)
Biến đổi vế trái ta có:
\(\frac{m^2-2mn+n^2}{m^2-n^2}=\frac{\left(m-n\right)^2}{\left(m-n\right)\left(m+n\right)}=\frac{m-n}{m+n}\)
=> VT=VP=\(\frac{m-n}{m+n}\) (đpcm)
c)\(\frac{a-b}{11}=\frac{3a\left(a-b\right)^2}{33a^2-33ab}\)
BĐ VP ta có:
\(\frac{3a\left(a-b\right)^2}{33a^2-33ab}=\frac{3a\left(a-b\right)^2}{33a\left(a-b\right)}=\frac{a-b}{11}\)
=> VT=VP=\(\frac{a-b}{11}\)(đpcm)
d) \(\frac{a^2+4ab+4b^2}{a^2-4b}=\frac{a+2b}{a-2b}\)
Bđ VT ta có:
\(\frac{a^2+4ab+4b^2}{a^2-4b}=\frac{\left(a+2b\right)^2}{\left(a-2b\right)\left(a+2b\right)}=\frac{a+2b}{a-2b}\)
=> VT=VP=\(\frac{a+2b}{a-2b}\)(đpcm)