Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: B
HD Giải:
P = R I 2 = R E 2 ( R + r ) 2 ⇔ 4 = R .6 2 ( R + 2 ) 2 ⇔ R 2 − 5 R + 4 = 0 ⇔ R 1 = 1 Ω , R 2 = 4 Ω

Đáp án: A
Ta có:
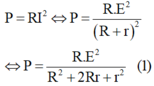
Thay E, P, r vào (1) ta có:
R 2 - 5R + 4 = 0 (2)
Giải phương trình (2) ta có:
R 1 = 1 Ω ; R 2 = 4 Ω

Đáp án B
P 1 = P 2 ⇔ E r + R 1 2 . R 1 = E r + R 1 + R 2 2 R 1 + R 2 ⇔ 1 3 + 1 2 = 1 + R 2 3 + 1 + R 2 2 ⇒ R 2 = 8 Ω .




Cường độ dòng diện trong mạch : \(I=\dfrac{\zeta}{R+r}=\dfrac{10}{R+r}\)
Công suất mạch ngoài : \(P=I^2R=\dfrac{100R}{\left(R+r\right)^2}\)
\(R=R_1;R_2\Rightarrow P=\dfrac{100R_1}{\left(R_1+r\right)^2}=\dfrac{100R_2}{\left(R_2+r\right)^2}=4\\ \Rightarrow\left\{{}\begin{matrix}\sqrt{R_1}\left(R_2+r\right)=\sqrt{R_2}\left(R_1+r\right)\left(1\right)\\\left(R_1+r\right)^2=25R_1\left(2\right)\end{matrix}\right.\\ \left(1\right)\Rightarrow\sqrt{R_1R_2}\left(\sqrt{R_2}-\sqrt{R_1}\right)=\left(\sqrt{R_2}-\sqrt{R_1}\right)r\\ \Rightarrow\sqrt{R_1R_2}=r=\sqrt{R_1\left(13-R_1\right)}\\ \left(2\right)\Rightarrow\left(R_1+\sqrt{R_1\left(13-R_1\right)}\right)^2=25R_1\\ \Rightarrow R_1^2+2R_1\sqrt{R_1\left(13-R_1\right)}+13R_1-R_1^2=25R_1\\ \Rightarrow2R_1\sqrt{R_1\left(13-R_1\right)}=12R_1\\ \Rightarrow R_1\left(13-R_1\right)=36\Rightarrow\left[{}\begin{matrix}R_1=9\Rightarrow R_2=4\\R_1=4\Rightarrow R_2=9\end{matrix}\right.\)
Vậy R1 ; R2 bằng \(9\left(\Omega\right);4\left(\Omega\right)\)