K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2022
\(z'_x=x^2-3\)
\(z'_y=1\)
\(z''_{xx}=2x\) ; \(z''_{xy}=0\) ; \(z''_{yy}=0\)
\(\Rightarrow d^2z=z''_{xx}dx^2+2z''_{xy}dxdy+z''_{yy}dy^2=2xdx^2\)
20.
\(-x^2+y=1\Rightarrow y=x^2+1\)
Thế vào hàm z ta được: \(z=\dfrac{x^3}{3}-3x+x^2+1\)
\(z'=x^2+2x-3=0\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=2\\x=-3\Rightarrow y=10\end{matrix}\right.\)
\(z''=2x+2\Rightarrow\left\{{}\begin{matrix}z''\left(1\right)=4>0\\z''\left(-3\right)=-4< 0\end{matrix}\right.\)
\(\Rightarrow M\left(-3;10\right)\) là điểm cực đại và \(N\left(1;2\right)\) là điểm cực tiểu
AM
10 tháng 2 2022
Ta có: \(\int\dfrac{xdx}{x^2+3}\)
Đặt \(u=x^2+3\left(u>0\right)\)
Có \(du=2xdx\)
\(\Rightarrow\int\dfrac{xdx}{x^2+3}=\)\(\int\dfrac{du}{2u}=\dfrac{1}{2}ln\left(u\right)=\dfrac{1}{2}ln\left(x^2+3\right)\)
TT
1
. Em cảm ơn
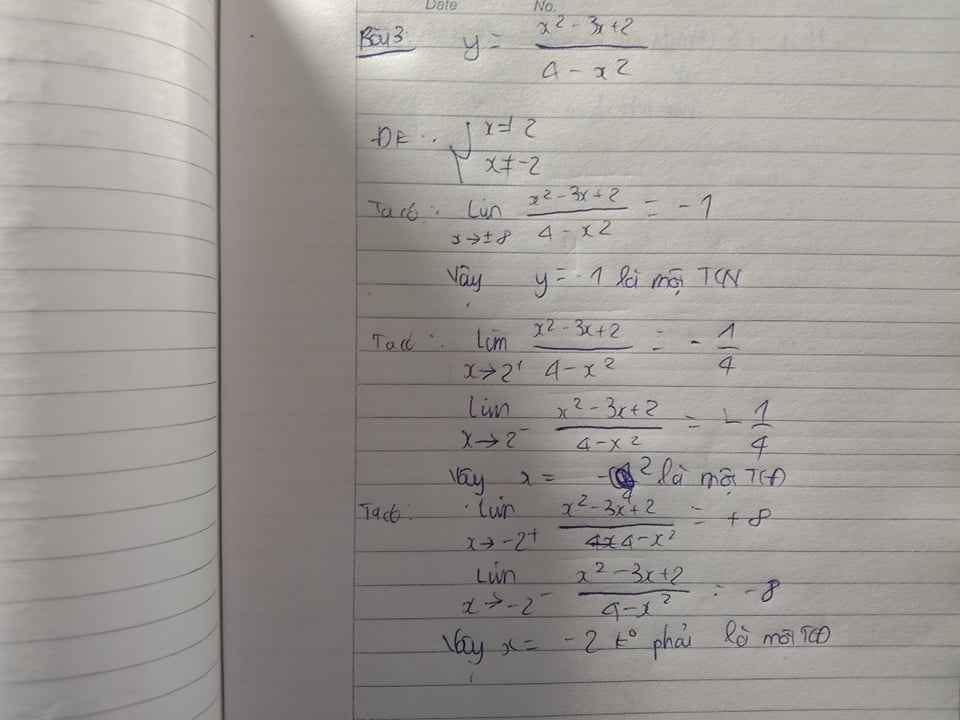
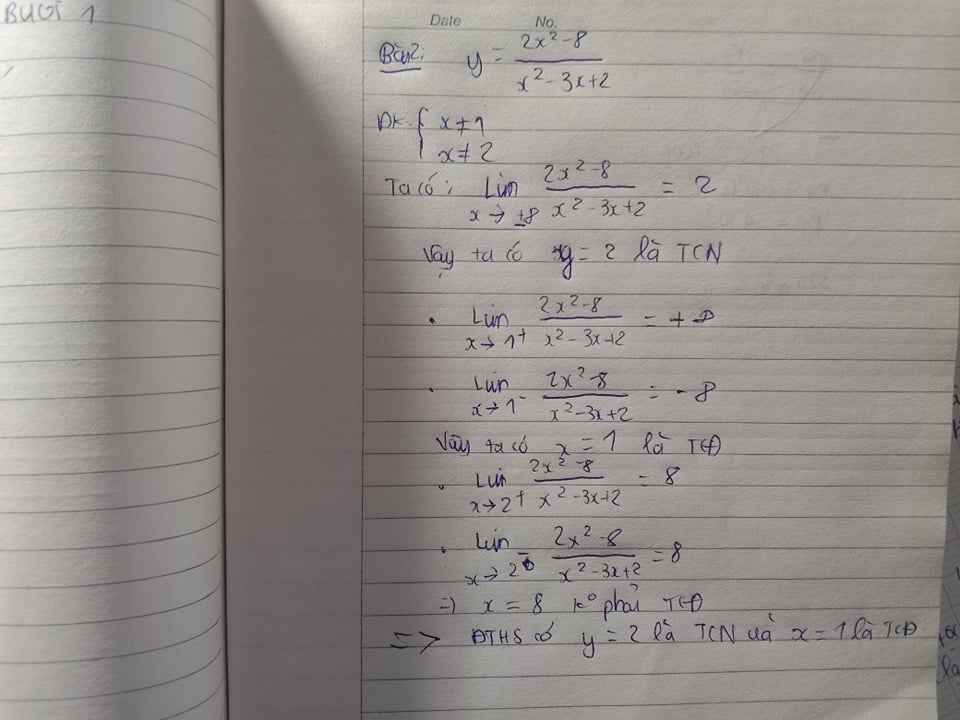
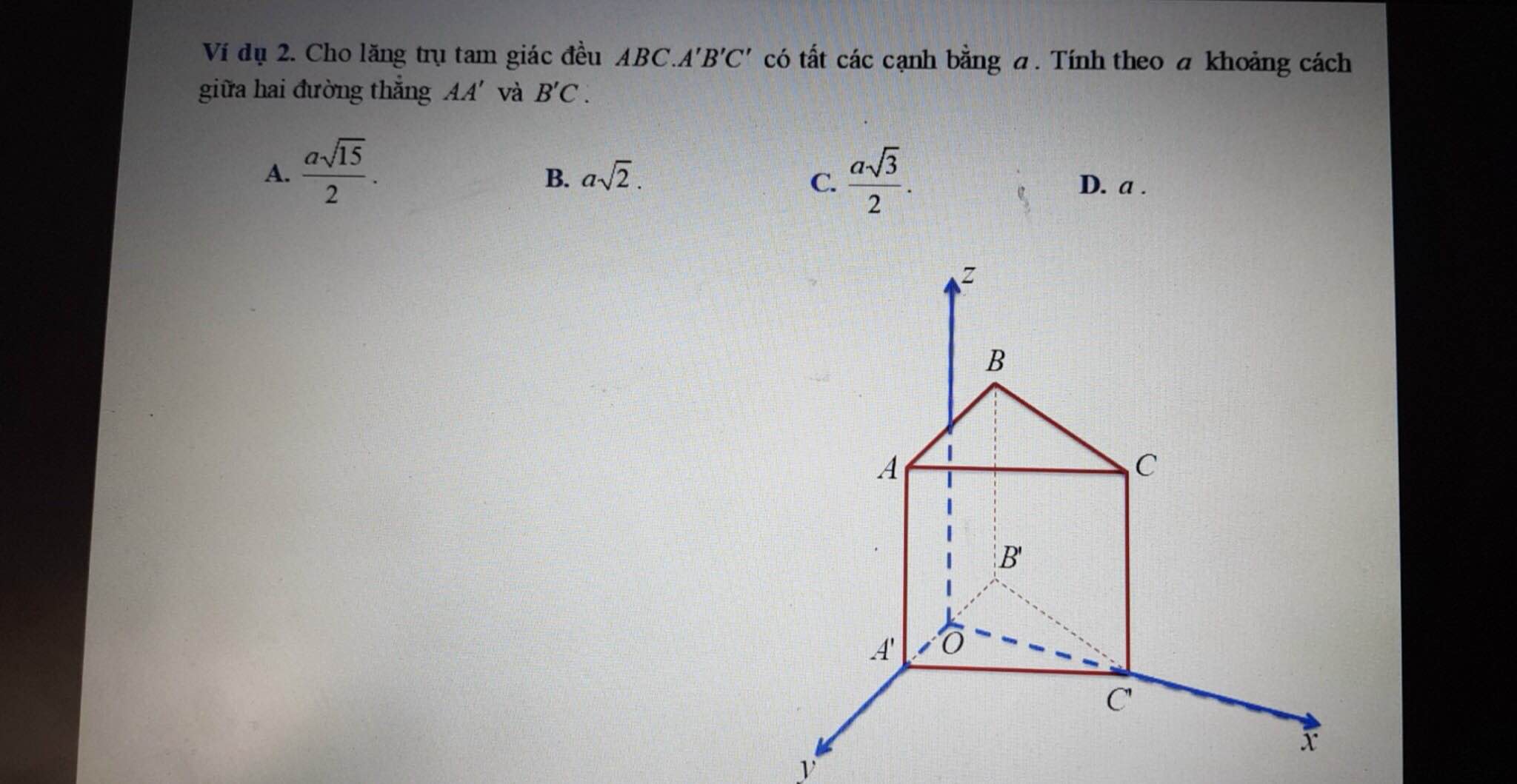
Đáp án C đúng rồi mà nhỉ.
Dạ vâng em cảm ơn ạ chắc đề sai ạ