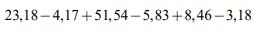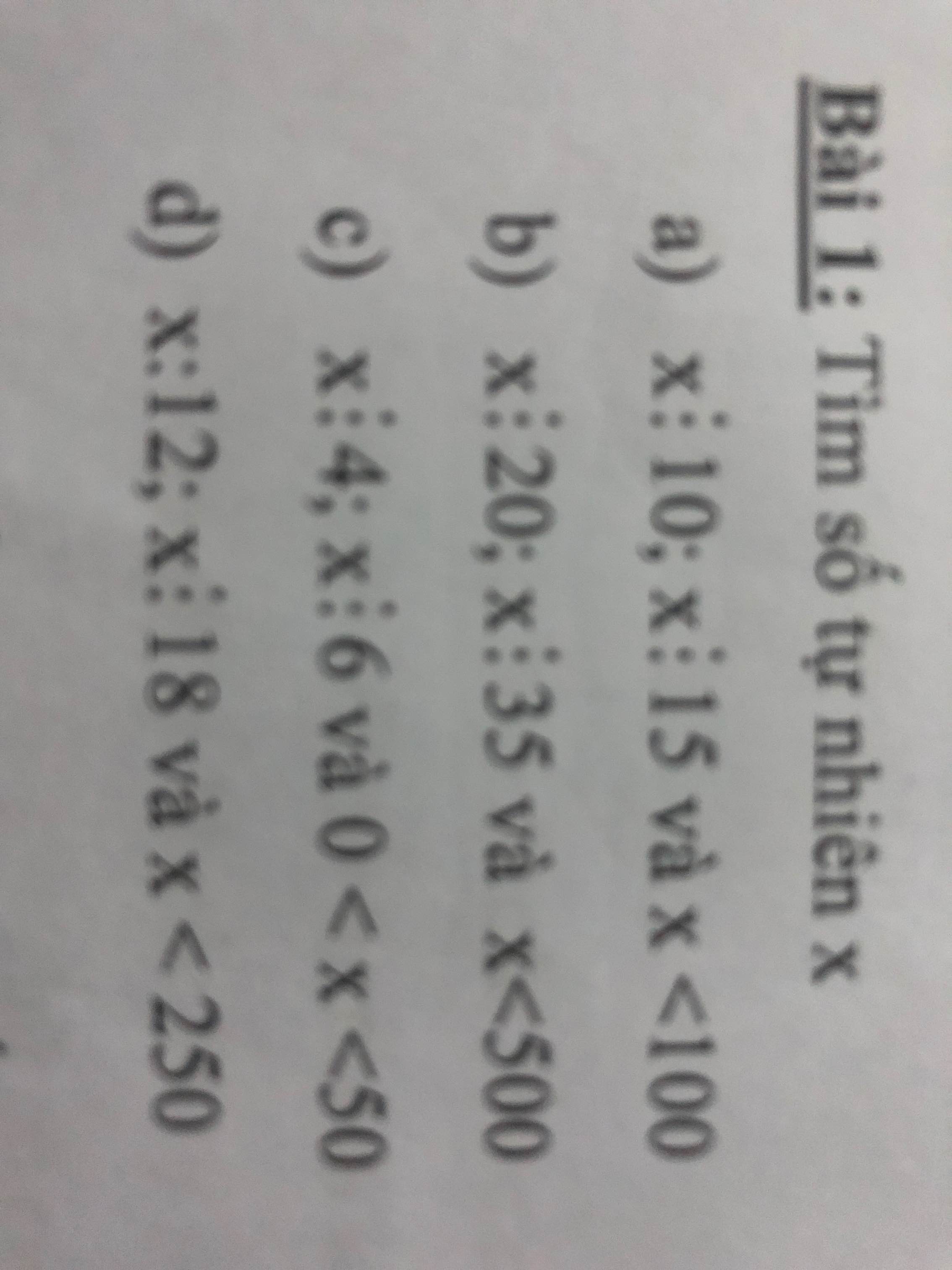Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)\(-1,6:\left(1+\dfrac{2}{3}\right)=-1,6:\dfrac{5}{3}=-\dfrac{8}{5}.\dfrac{3}{5}=\dfrac{-24}{25}\)
b)\(\left(\dfrac{-2}{3}\right)+\dfrac{3}{4}-\left(-\dfrac{1}{6}\right)+\left(\dfrac{-2}{5}\right)=-\dfrac{2}{3}+\dfrac{3}{4}+\dfrac{1}{6}-\dfrac{2}{5}=\dfrac{-40+45+10-24}{60}=\dfrac{-9}{60}=\dfrac{-3}{20}\)
c)\(\left(\dfrac{-3}{7}:\dfrac{2}{11}+\dfrac{-4}{7}:\dfrac{2}{11}\right).\dfrac{7}{33}=\left(\dfrac{-3}{7}.\dfrac{11}{2}+\dfrac{-4}{7}.\dfrac{11}{2}\right).\dfrac{7}{33}=\left[\dfrac{11}{2}\left(\dfrac{-3}{7}+\dfrac{-4}{7}\right)\right].\dfrac{7}{33}=\dfrac{-11}{2}.\dfrac{7}{33}=\dfrac{-7}{6}\)
d)\(\dfrac{-5}{8}+\dfrac{4}{9}:\left(\dfrac{-2}{3}\right)-\dfrac{7}{20}.\left(\dfrac{-5}{14}\right)=\dfrac{-5}{8}-\dfrac{4}{9}.\dfrac{3}{2}+\dfrac{1}{8}=\dfrac{-5}{8}+\dfrac{1}{8}-\dfrac{2}{3}=-\dfrac{7}{6}\)


12 : {390 : [500 - (125 + 35 . 7)]}
= 12 : {390 : [500 - (125 + 245)]}
= 12 : [390 : (500 - 370)]
= 12 : (390 : 130)
= 12 : 3
= 4
12 : { 390 : [ 500 - ( 125 + 35. 7 ) ] }
= 12 : { 390 : [ 500 - ( 125 + 245 ) ] }
= 12 : { 390 : [ 500 - 370 ] }
= 12 : { 390 : 130 }
= 12 : 3
= 4


= 23,18 - 3,18 - 4,17 - 5,83 + 51,54 + 8,46
= 20 - 10 + 60
= 70


a: \(x\in\left\{30;60;90\right\}\)
b: \(x\in\left\{140;280;420\right\}\)


\(a,A=2^0+2^1+2^2+...+2^{2006}\\ \Rightarrow2A=2^1+2^2+...+2^{2007}\\ \Rightarrow2A-A=2^1+2^2+...+2^{2007}-2^0-2^1-...-2^{2006}\\ \Rightarrow A=2^{2007}-1\)
\(b,B=1+3+3^2+...+3^{100}\\ \Rightarrow3B=3+3^2+...+3^{101}\\ \Rightarrow3B-B=3+3^2+...+3^{101}-1-3-3^2-...-3^{100}\\ \Rightarrow2B=3^{101}-1\\ \Rightarrow B=\dfrac{3^{101}-1}{2}\)

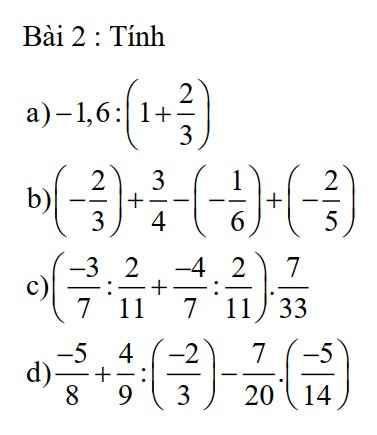 giúp với giúp với giúp e với ạ. e cảm ơn
giúp với giúp với giúp e với ạ. e cảm ơn