
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c) \(\left(\dfrac{\sqrt{x}}{2\sqrt{x}-2}-\dfrac{\sqrt{x}}{2\sqrt{x}+2}\right):\dfrac{\sqrt{x}}{x+2\sqrt{x}+1}\)
= \(\left(\dfrac{\sqrt{x}}{2\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}}{2\left(\sqrt{x}+1\right)}\right):\dfrac{\sqrt{x}}{\sqrt{x}^2+2\sqrt{x}+1^2}\)
= \(\left(\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\) \(:\dfrac{\sqrt{x}}{\left(\sqrt{x}+1\right)^2}\)
= \(\left(\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)-\sqrt{x}\left(\sqrt{x}-1\right)}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\) \(.\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}}\)
= \(\dfrac{2\sqrt{x}}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}}\)
= \(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
Chúc bạn học tốt

b: \(Q=\dfrac{x+5}{\sqrt{x}+2}=\dfrac{x-4}{\sqrt{x}+2}+\dfrac{9}{\sqrt{x}+2}=\sqrt{x}-2+\dfrac{9}{\sqrt{x}+2}\)
\(=\sqrt{x}+2+\dfrac{9}{\sqrt{x}+2}-4\)
\(\Leftrightarrow Q\ge2\sqrt{9}-4=2\cdot3-4=2\)
Dấu '=' xảy ra khi x=1

a.
\(\Delta=\left(-5\right)^2-4.3.2=25-24=1>0\)
\(\Rightarrow\) Phương trình có 2 nghiệm pb
b.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{5}{3}\\x_1x_2=\dfrac{2}{3}\end{matrix}\right.\)
\(4A=x_1^2+x_2^2-x_1x_2=\left(x_1^2+x_2^2+2x_1x_2\right)-3x_1x_2\)
\(4A=\left(x_1+x_2\right)^2-3x_1x_2\)
\(4A=\left(\dfrac{5}{3}\right)^2-3.\left(\dfrac{2}{3}\right)=\dfrac{7}{9}\)
\(\Rightarrow A=\dfrac{7}{36}\)



Bài làm:
Ta có: \(\sin B=\frac{4}{5}\Leftrightarrow\frac{AC}{BC}=\frac{4}{5}\) => \(AC=\frac{4}{5}BC=\frac{4}{5}.a\sqrt{5}=\frac{4a\sqrt{5}}{5}\)
Áp dụng định lý Pytago ta tính được:
\(AB=\sqrt{BC^2-AC^2}=\sqrt{5a^2-\frac{16}{5}a^2}=\sqrt{\frac{9}{5}a^2}=\frac{3a\sqrt{5}}{5}\)
Mà \(AH.BC=AB.AC\) => \(AH=\frac{AB.AC}{BC}=\frac{\frac{4a\sqrt{5}}{5}\cdot\frac{3a\sqrt{5}}{5}}{a\sqrt{5}}=\frac{12a\sqrt{5}}{25}\)
Áp dụng công thức ta tính được:
\(BH=\frac{AB^2}{BC}=\frac{\left(\frac{3a\sqrt{5}}{5}\right)^2}{a\sqrt{5}}=\frac{9a\sqrt{5}}{25}\)
\(CH=\frac{AC^2}{BC}=\frac{\left(\frac{4a\sqrt{5}}{5}\right)^2}{a\sqrt{5}}=\frac{16a\sqrt{5}}{25}\)
Vậy \(AB=\frac{3a\sqrt{5}}{5}\) ; \(AC=\frac{4a\sqrt{5}}{5}\) ; \(AH=\frac{12a\sqrt{5}}{25}\) ; \(BH=\frac{9a\sqrt{5}}{25}\) ; \(CH=\frac{16a\sqrt{5}}{25}\)


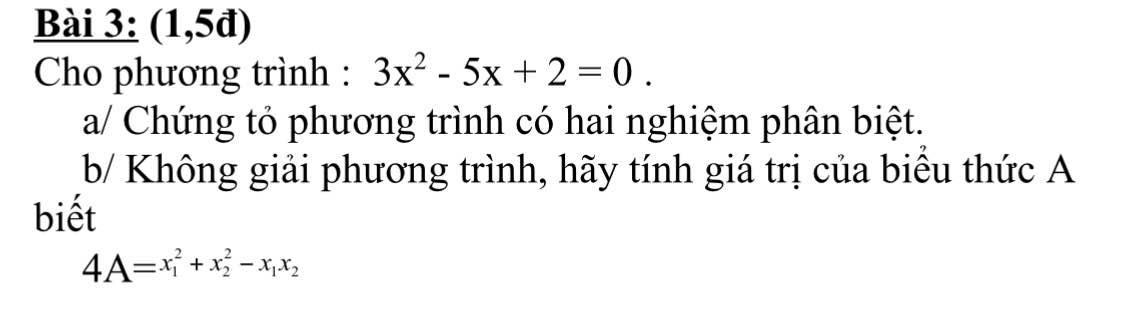

????
Tkông kẻm lỗi á:)