
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


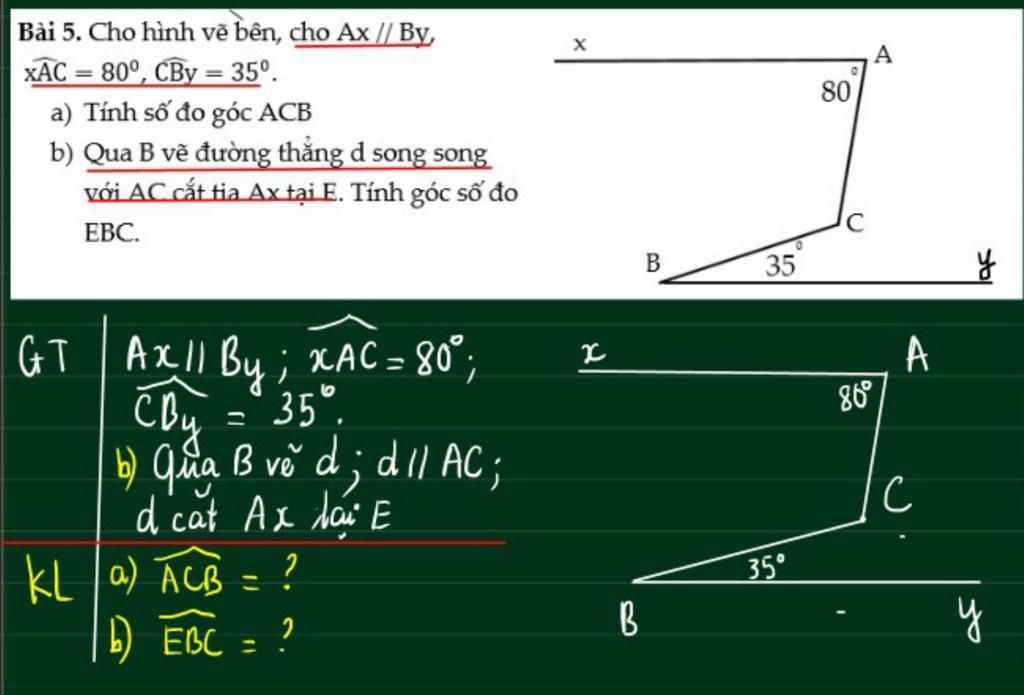
a, Giả sử: Cz // Ax // By
Do Cz // Ax \(\Rightarrow\widehat{A}+\widehat{C_1}=180^o\)(2 góc TCP)
\(\Rightarrow80^o+\widehat{C_1}=180^o\)
\(\Rightarrow\widehat{C_1}=180^o-80^o=100^o\)
Do Cz // By \(\Rightarrow\widehat{C_2}=\widehat{B}=35^o\)(2 góc so le trong)
Ta thấy: \(\widehat{ACB}=\widehat{C_1}+\widehat{C_2}=100^o+35^o=135^o\)
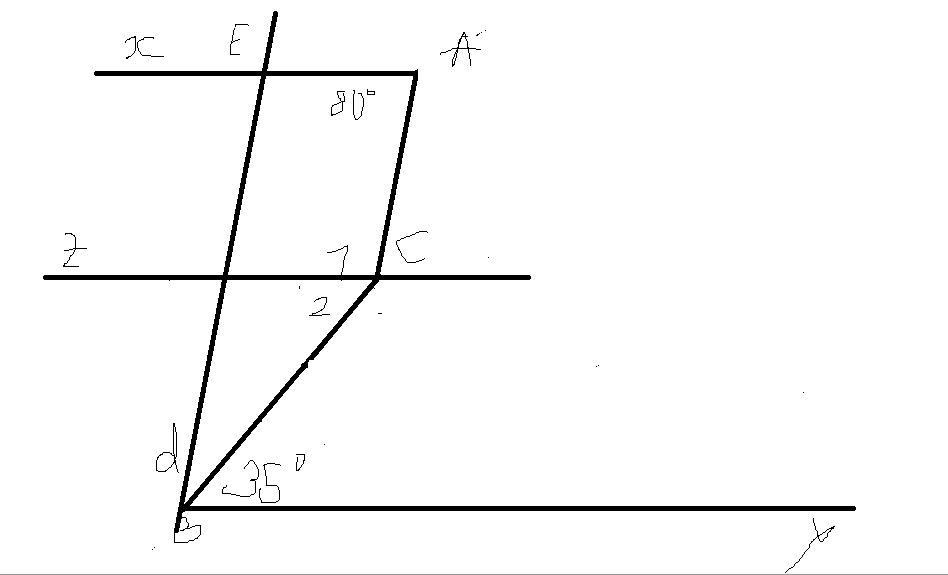
b, Do d // AC \(\Rightarrow\widehat{ACB}+\widehat{EBC}=180^o\)(2 góc TCP)
\(\Rightarrow135^o+\widehat{EBC}=180^o\)
\(\Rightarrow\widehat{EBC}=180^o-135^o=45^o\)

a: góc ACB=180-50-65=65 độ
b: góc xAy=góc ABC=65 độ
góc xAC=180-65-50=65 độ
=>góc xAy=góc xAC
=>Ax là phân giác của góc yAC

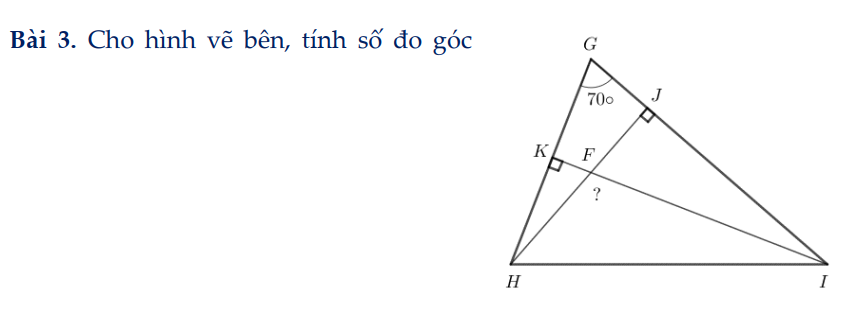
tam giác KGI vuông tại K có
góc GIK = 90 độ - góc KGI
góc GIK = 90 độ - 70 độ = 20 độ
=> góc IFJ = 90 độ - góc GIK
góc IFJ = 90 độ - 20 độ =70 độ
góc HFI = 180 độ - góc IFJ
góc HFI = 180 độ - 70 độ = 110 độ

\(b,\dfrac{1}{2}+\dfrac{13}{19}-\dfrac{4}{9}+\dfrac{6}{19}+\dfrac{5}{18}\\ =\left(\dfrac{1}{2}+\dfrac{5}{18}\right)+\left(\dfrac{13}{19}+\dfrac{6}{19}\right)-\dfrac{4}{9}\\ =\left(\dfrac{9}{18}+\dfrac{5}{18}\right)+\dfrac{19}{19}-\dfrac{4}{9}\\ =\dfrac{14}{18}+1-\dfrac{4}{9}\\ =\dfrac{7}{9}+1-\dfrac{4}{9}\\ =\left(\dfrac{7}{9}-\dfrac{4}{9}\right)+1\\ =\dfrac{3}{9}+1\\ =\dfrac{1}{3}+1\\ =\dfrac{4}{3}\)
\(c,\dfrac{-20}{23}+\dfrac{2}{3}-\dfrac{3}{23}+\dfrac{2}{5}+\dfrac{7}{15}\\ =\left(-\dfrac{20}{23}-\dfrac{3}{23}\right)+\left(\dfrac{2}{5}+\dfrac{7}{15}\right)+\dfrac{2}{3}\\ =-\dfrac{23}{23}+\left(\dfrac{6}{15}+\dfrac{7}{15}\right)+\dfrac{2}{3}\\ =-1+\dfrac{13}{15}+\dfrac{2}{3}\\ =-\dfrac{15}{15}+\dfrac{13}{15}+\dfrac{10}{15}\\ =\dfrac{8}{15}\)
\(e,\dfrac{5}{7}.\dfrac{5}{11}+\dfrac{5}{7}.\dfrac{2}{11}-\dfrac{5}{7}.\dfrac{14}{11}\\ =\dfrac{5}{7}.\left(\dfrac{5}{11}+\dfrac{2}{11}-\dfrac{14}{11}\right)\\ =\dfrac{5}{7}.\dfrac{-7}{11}\\ =-\dfrac{35}{77}\\ =-\dfrac{5}{11}\)
\(f,\dfrac{2}{11}.\dfrac{-5}{4}+\dfrac{-9}{11}.\dfrac{5}{4}+1\dfrac{3}{4}\\ =-\dfrac{2}{11}.\dfrac{5}{4}+\dfrac{-9}{11}.\dfrac{5}{4}+\dfrac{7}{4}\\=\dfrac{5}{4}.\left(-\dfrac{2}{11}+\dfrac{-9}{11}\right)+\dfrac{7}{4}\\ =\dfrac{5}{4}.1+\dfrac{7}{4}\\ =\dfrac{5}{4}+\dfrac{7}{4}\\=\dfrac{12}{4}\\ =3\)
\(h,\dfrac{7}{4}\cdot\dfrac{29}{5}-\dfrac{7}{5}\cdot\dfrac{9}{4}+3\dfrac{2}{13}\\ =\dfrac{7}{4}\cdot\dfrac{29}{5}-\dfrac{7}{4}\cdot\dfrac{9}{5}+\dfrac{41}{13}\\ =\dfrac{7}{4}\cdot\left(\dfrac{29}{5}-\dfrac{9}{5}\right)+\dfrac{41}{13}\\ =\dfrac{7}{4}\cdot\dfrac{20}{5}+\dfrac{41}{13}\\ =\dfrac{7}{4}.4+\dfrac{41}{13}\\ =\dfrac{28}{4}+\dfrac{41}{13}\\ =7+\dfrac{41}{13}\\ =\dfrac{132}{13}\)

1. a) \(13.146-46.13+4^2.5-6\left(3^2-4\right)=13\left(146-46\right)+16.5-6.5\)
\(=13.100+5\left(16-6\right)\)
\(=13.100+5.10=135\)
b) \(35+\left[149-2\left(3^3.19-3^3.17\right)\right]=35+\left[149-2.3^3\left(19-17\right)\right]\)
\(=35+149-54.2\)
\(=76\)
2. a) \(5\left(x+15\right)=5^3\Leftrightarrow x+15=5^2\Leftrightarrow x=10\)
Vậy \(x=10\)
b) Không nhìn được
2:
a: 5(x+15)=5^3
=>x+15=5^3/5=25
=>x=10
b: 23+x-3^2=5^3-5^4
=>x+14=125-625=-500
=>x=-500-14=-514

\(\frac{2^7.9^2}{3^3.2^5}\)
\(=\frac{2^7.\left(3^2\right)^2}{3^3.2^5}\)
\(=\frac{2^7.3^4}{3^3.2^5}\)
\(=2^2.3=4.3=12\)
\(\frac{2^7.9^2}{3^3.2^5}=\frac{2^7.\left(3.3\right)^2}{3^3.2^5}=\frac{2^7.3^2.3^2}{3^3.2^5}=\frac{2^2.3}{1}=12\)

Câu 2:
a, Vì m⊥MN và n⊥MN nên m//n
b, Vì m//n nên \(\widehat{D_1}=\widehat{C}=45^0\) (so le trong)
c, Vì m//n nên \(\widehat{D_1}=\widehat{C_1}\) (đồng vị)

a) \(\Rightarrow\left(x-3\right)\left(x+4\right)=5.12\)
\(\Rightarrow x^2+x-72=0\)
\(\Rightarrow\left(x-8\right)\left(x+9\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=8\\x=-9\end{matrix}\right.\)
b) \(\Rightarrow\left(x+3\right)^2=36\)
\(\Rightarrow\left[{}\begin{matrix}x+3=6\\x+3=-6\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-9\end{matrix}\right.\)
c) \(\Rightarrow2x^2=8\Rightarrow x^2=4\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)

\(1+2+...+n=\dfrac{\left(\dfrac{n-1}{1}+1\right).\left(n+1\right)}{2}=\dfrac{n\left(n+1\right)}{2}\)
\(M=\dfrac{3}{1+2}+\dfrac{3}{1+2+3}+...+\dfrac{3}{1+2+...+2022}\)
\(=3\left(\dfrac{1}{1+2}+\dfrac{1}{1+2+3}+...+\dfrac{1}{1+2+...+2022}\right)\)
\(=3\left(\dfrac{1}{\dfrac{2.\left(2+1\right)}{2}}+\dfrac{1}{\dfrac{3.\left(3+1\right)}{2}}+...+\dfrac{1}{\dfrac{2022.\left(2022+1\right)}{2}}\right)\)
\(=3\left(\dfrac{2}{2.3}+\dfrac{2}{3.4}+...+\dfrac{2}{2022.2023}\right)\)
\(=3.2.\left(\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{2022.2023}\right)\)
\(=6.\left(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2022}-\dfrac{1}{2023}\right)\)
\(=6.\left(\dfrac{1}{2}-\dfrac{1}{2023}\right)\)
\(=6.\dfrac{2021}{4046}=3.\dfrac{2021}{2023}=\dfrac{6063}{2023}=\dfrac{18189}{6069}\)
\(\dfrac{10}{3}=\dfrac{20230}{6069}>\dfrac{18189}{6069}=M\)

 cần gấp
cần gấp giúp em với ạ e, đang cần gấp lắm ạ
giúp em với ạ e, đang cần gấp lắm ạ

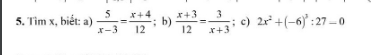
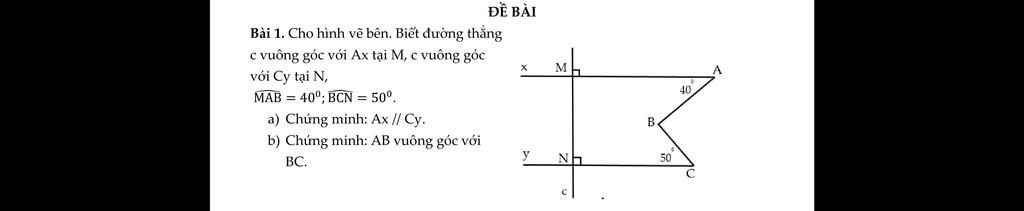
a, Do MN ⊥ Ax , MN ⊥ Cy => Ax // Cy ( từ vuông góc đến song song)
b, Kẻ Bz // AB // Cy
Do Ax // Bz \(\Rightarrow\widehat{A}=\widehat{B_1}=40^o\)(2 góc so le trong)
Do Bz // Cy \(\Rightarrow\widehat{B_2}=\widehat{C}=50^o\)
Ta thấy: \(\widehat{ABC}=\widehat{B_1}+\widehat{B_2}=40^o+50^o=90^ohayAB\perp BC\left(dpcm\right)\)