Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Không gian mẫu là tập hợp số chấm xuất hiện khi gieo con xúc xắc hai lần liên tiếp khi đó \(n\left( \Omega \right) = 6.6 = 36\)
A = {(1; 1); (1; 2); (1; 3); (1; 4); (1; 5); (1; 6)} \( \Rightarrow P\left( A \right) = \frac{6}{{36}} = \frac{1}{6}\)
B = {(1; 2); (2; 2); (3; 2); (4; 2); (5; 2); (6; 2)} \( \Rightarrow P\left( B \right) = \frac{6}{{36}} = \frac{1}{6}\)
C = {(2; 6); (3; 5); (4; 4); (5; 3); (6; 2)} \( \Rightarrow P\left( C \right) = \frac{5}{{36}}\)
D = {(1; 6); (2; 5); (3; 4); (4; 3); (5; 2); (6; 1)} \( \Rightarrow P\left( D \right) = \frac{6}{{36}} = \frac{1}{6}\)
Do đó
\(P\left( A \right).P\left( C \right) = \frac{1}{6}.\frac{5}{{36}} = \frac{5}{{216}};P\left( B \right).P\left( C \right) = \frac{1}{6}.\frac{5}{{36}} = \frac{5}{{216}};P\left( C \right).P\left( D \right) = \frac{5}{{36}}.\frac{1}{6} = \frac{5}{{216}}\)
Mặt khác
AC = \(\emptyset \Rightarrow P\left( {AC} \right) = 0\)
BC = {(6; 2)} \( \Rightarrow P\left( {BC} \right) = \frac{1}{{36}}\)
CD = \(\emptyset \Rightarrow P\left( {CD} \right) = 0\)
Khi đó \(P\left( {AC} \right) \ne P\left( A \right).P\left( C \right);P\left( {BC} \right) \ne P\left( B \right).P\left( C \right);P\left( {CD} \right) \ne P\left( C \right).P\left( D \right)\)
Vậy các cặp biến cố A và C; B và C, C và D không độc lập.

Đáp án A
Số phần tử của không gian mẫu: ![]()
Gọi A là biến cố mặt 6 chấm không xuất hiện.
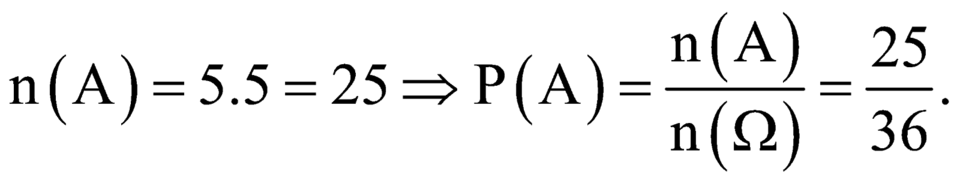

Đáp án B
Phương pháp:
Phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có nghiệm
⇔ ∆ ≥ 0

![]()
![]()
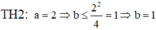
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Gọi A là biến cố:
"Phương trình a x 2 + b x + c = 0 có nghiệm"
![]()
![]()

Xác suất:
a. \(\dfrac{3}{6}.\dfrac{3}{6}=\dfrac{1}{4}\)
b. \(\dfrac{6}{36}=\dfrac{1}{6}\)
c. Xác suất mặt 6 chấm ko xuất hiện lần nào: \(\dfrac{5}{6}.\dfrac{5}{6}=\dfrac{25}{36}\)
Xác suất mặt 6 xuất hiện ít nhất 1 lần: \(1-\dfrac{25}{36}=\dfrac{11}{36}\)
d. Các trường hợp tổng 2 mặt lớn hơn hoặc bằng 10: (6;4), (4;6); (5;5); (5;6);(6;5);(6;6) có 6 khả năng
\(\Rightarrow36-6=30\) khả năng tổng số chấm bé hơn 10
Xác suất: \(\dfrac{30}{36}=\dfrac{5}{6}\)