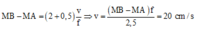Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A,B là 2 nguồn cùng pha nên đường trung trực của AB dao động cực đại.
Giữa M và đường trung trực của AB có 3 dãy dực đại khác => M nằm trên dãy cực đại k = 4
\(d_2-d_1=(k+\frac{\triangle\varphi}{2\pi})\lambda = (4+0)\lambda \Rightarrow \lambda = \frac{d_2-d_1}{4}=\frac{21-19}{4}=0.5cm \Rightarrow v = f.\lambda = 80.0,5=40cm/s.\)

Bước sóng \(\lambda = v/f = 1/25 = 0.04m = 4cm.\)
Độ lệch pha giữa hai nguồn sóng là \(\triangle\varphi= \varphi_2-\varphi_1 = \frac{5\pi}{6}+\frac{\pi}{6} = \pi.\)
Biên độ sóng tại điểm M là \( A_M = |2a\cos\pi(\frac{10-50}{4}-\frac{\pi}{2\pi})| =0.\)

+ M là một cực tiểu giao thoa, giữa M và trung trực AB có hai dãy cực đại → M thuộc cực tiểu ứng với k = 2.
Ta có
MB - MA = (2+0,5) v f ⇒ v = ( M B - M A ) f 2 , 5 = 20 cm/s
Đáp án A

\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)

\(\Delta\varphi=\omega\frac{x_2-x_1}{v}=5\pi\)
hai giao động ngược pha
Đáp án A
+ M là một cực tiểu giao thoa, giữa M và trung trực AB có hai dãy cực đại M thuộc cực tiểu với k = 2
Ta có