Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
\(\dfrac{i_1}{i_2}=\dfrac{\lambda_1}{\lambda_2}=\dfrac{2}{3}\)
Theo giả thiết:
\(x_M=6i_1=6.\dfrac{2}{3}i_2=4i_2\)
\(x_N=6i_2=6.\dfrac{3}{2}i_1=9i_1\)
Như vậy, trung điểm I có tọa độ: \(x_I=7,5i_1=5i_2\)
Do đó, trong khoảng giữa I và N có vân i1 là: \(8i_1\), và không có vân i2 nào
Như vậy, tổng cộng có 1 vân sáng.

M, N là hai vân sáng, trên đoạn MN có 10 vân tối => có 11 vân sáng. Tức là có 10 khoảng vân.
\(10i_1 = 20 mm=> i_1 = 2mm.\)
\(\frac{i_1}{i_2}= \frac{\lambda_1}{\lambda_2}= \frac{3}{5}=> i_2 = \frac{10}{3}mm.\)
Nhận xét: \(\frac{MN}{i_2}= 6\)=> có 7 vân sáng.

Số vân sáng trong khoảng MN chính là số k thỏa mãn
\(x_M < x_s < x_N\)
=> \( 2 < k i < 4,5 \)
=> \(1,67 < k < 3,75.\)
Do \(k \in Z \) => \( k = 2,3.\)
Tương tự.
Số vân tối trong khoảng MN chính là số k thỏa mãn
\(x_M < x_t < x_N\)
=> \( 2 < (k+\frac{1}{2})i < 4,5\)
=> \( 1,167 < k < 3,25.\)
Do \(k \in Z \) => \(k = 2,3.\)
Vẫn chưa hiểu tại đoạn: k∈Z => k=2,3. Ai giải thích cho mình với ạ.

Theo đề bài: Với bức xạ λ1 thì 10i1 = MN = 20mm → i1 = 2mm.
\(\frac{\iota_1}{\iota_2}=\frac{\text{λ}_1}{\text{λ}_2}=\frac{3}{5}\)\(\rightarrow\iota_2=\frac{10}{3}mm\rightarrow N_2=2.\left[\frac{MN}{2\iota_2}\right]+1=7\)

Chọn đáp án D
Các bức xạ đều cho vân sáng bậc k = 0 tại tại O ⇒vân trung tâm O là một vân trùng. Tại điểm M ≠O trên màn vân sáng của hai bức xạ trùng nhau thì ta có OM = k 1 i 1 = k 2 i 2 ( k 1 , k 2 nguyên dương)
⇒ k 1 λ 1 = k 2 λ 2 ⇒ k 1 k 2 = λ 2 λ 1 = 5 6 ⇒ k 1 chia hết cho 5, k 2 chia hết cho 6.
Vân trùng gần vân trung tâm nhất cách vân trung tâm một khoảng
i’ = k 1 min . i 1 = 5. λ 1 D a = 6 m m , các vân trùng nằm phân bố đều đặn trên màn và khoảng cách giữa hai vân trùng liên tiếp bằng i’= 6 mm.
Ta có L 2. i ' = 2 , 33
→ số vân trùng của hai bức xạ trên màn bằng n = 2 L 2 i ' + 1 = 2.2 + 1 = 5 vân.

Các bức xạ đều cho vân sáng bậc k = 0 tại tại O ⇒ vân trung tâm O là một vân trùng. Tại điểm M ≠ O trên màn vân sáng của hai bức xạ trùng nhau thì ta có
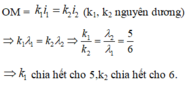
Vân trùng gần vân trung tâm nhất cách vân trung tâm một khoảng
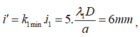
các vân trùng nằm phân bố đều đặn trên màn và khoảng cách giữa hai vân trùng liên tiếp bằng i’= 6 mm
→ số vân trùng của hai bức xạ trên màn bằng
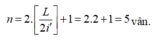
Đáp án A

Đáp án: 23 vị trí; 0,6mm.
Cách 1:
- Vân sáng của i1 trùng với vân tối của i2 →2i1 = 0,6mm; i2 = 0,4; i0 = 1,2mm;
- Ta có kM = -4,6; kN = 18,3. Số giá trị k bán nguyên là : 17,5 + 4,5 + 1 = 23 giá trị.
Cách 2:
+ Vân sáng của λ1 trùng với vân sáng của λ2: \(\frac{k_1}{k_2}=\frac{i_1}{i_2}=\frac{4}{3}\)
\(\Rightarrow\) Vân sáng có tọa độ 4ki1 của λ1 trùng với vân sáng có tọa độ 3ki2của λ2
\(\Rightarrow\) Vân sáng có tọa độ 2ki1 của λ1 trùng với vân sáng có tọa độ 1,5 ki2của λ2 (k lẻ)
\(\Rightarrow\) xtrùng = \((k+\frac{1}{2})4i_1(mm) \Rightarrow 5,5\leq(k+\frac{1}{2})4i_1\leq 2,2.10\)
\(\Leftrightarrow{-5,08}\leq{k}\leq{17,8}\)
\(\Rightarrow\) có 23 vị trí thỏa mãn.
Khoảng cách gần nhất từ điểm thỏa mãn đến vân trung tâm tương ứng với k = 0
xmin = 0,5.4i1 = 0,6 (mm)

Cách giải: Đáp án D
Ta có

Vậy tại M lúc sau phải là vị trí của vân tối của λ2.Từ kết quả trên ta suy ra: MN = 10i1 =14i2 .Vậy trên đoạn MN có 15 vân tối.

Giả sử ta dịch vân sáng trung tâm về M thì N là vị trí vân sáng thứ 10(có 10 vân tối)
\(\Rightarrow i_1=2mm\) , Khi thay \(\lambda_1\) bằng \(\lambda_2\) \(\Rightarrow\frac{i_1}{i_2}=\frac{\lambda_1}{\lambda_2}\Rightarrow i_2=\frac{i_1\lambda_2}{\lambda_1}=\frac{10}{3}mm\)
M là vị trí của 1 vân giao thoa,Ta có:
Vân trung tâm trên màn không đổi⇒ta tìm vị trí trùng nhau của 2 loai ánh sáng với 2 khoảng vân khác nhau hay tương ứng với khoảng cách từ vân trung tâm tới M.Ta chia 2 TH như sau:
TH1: M là vân tối
\(\frac{10}{3}.\left(n,5\right)=2k\) với n,k nguyên thì phương trình vô nghiệm
TH2:M là vân sáng
\(\frac{10}{3}.x=2y\)
ới x,y nguyên thì phương trình có nghiệm (3;5) và (6;10)
cả 2 nghiệm này đều kết luận trên MN có 7 vân sáng
----->chọn A