Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: 2SOAB = AB.OH = AB (vì OH = 1).
Vậy diện tích ∆OAB nhỏ nhất khi AB có độ dài ngắn nhất.
Vì AB = AH + HB mà AH.HB = OH2 = 1 nên AB có giá trị nhỏ nhất khi AH = HB tức ∆OAB vuông cân: OA = OB và
AB = 2AH = 2OH = 2.
AB2 = 4 = 2OA2 = 2OH = OA = OB = √2.
Khi đó tọa độ của A, B là A(√2; 0) và B(0; √2).

Ta có : HA.HB=OH²=1 (không đổi).
và AB=HA+HB ≥ 2√(HA.HB) = 2.√OH² = 2.
-> AB ≥ 2.
Vậy AB có độ dài nhỏ nhất là 2 khi HA=HB
Khi đó tg OHB và OHA vuông cân và có cạnh góc vuông = 1.
suy ra OA = OB =√2.
Vậy đoạn AB nhỏ nhất khi A(√2;0) B(0;√2).

Ta có : HA.HB=OH²=1 (không đổi).
và AB=HA+HB ≥ 2√(HA.HB) = 2.√OH² = 2.
-> AB ≥ 2.
Vậy AB có độ dài nhỏ nhất là 2 khi HA=HB
Khi đó tg OHB và OHA vuông cân và có cạnh góc vuông = 1.
suy ra OA = OB =√2.
Vậy đoạn AB nhỏ nhất khi A(√2;0) B(0;√2).
tick cho mk nha

Ta có:
\(396:9=44< 45\\ 370:8=46,25>45\\ 345:8=43,125< 45\)
Vậy khối 11 thống kê bị sai.

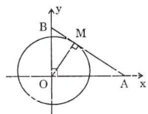
Gọi tiếp điểm của AB và đường tròn tâm O, bán kính 1 là M, ta có: OM ⊥ AB.
ΔOAB vuông tại O, có OM là đường cao nên MA.MB = MO2 = 1 (hằng số)
Áp dụng bất đẳng thức Cô-si ta có:
MA + MB ≥ 2√MA.MB = 2. √1 = 2
Dấu « = » xảy ra khi MA = MB = 1.
Khi đó OA = √(MA2 + MO2) = √2 ; OB = √(OM2 + MB2) = √2.
Mà A, B nằm trên tia Ox và Oy nên A(√2; 0); B(0; √2)
Vậy tọa độ là A(√2, 0) và B(0, √2).

\(\left\{{}\begin{matrix}k\ne-2\\\Delta'=k^2+k\left(k+2\right)>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}k\ne-2\\\left[{}\begin{matrix}k\ge0\\k\le-1\end{matrix}\right.\end{matrix}\right.\)
Theo định lý Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=\frac{2k}{k+2}\\x_1x_2=\frac{-k}{k+2}\end{matrix}\right.\)
\(\frac{x_1+x_2}{2}=1\)
\(\Leftrightarrow x_1+x_2=2\)
\(\Leftrightarrow\frac{2k}{k+2}=2\)
\(\Leftrightarrow2k=2k+4\)
Không tồn tại k thỏa mãn
Gần như không có ai đầu top mà không buff bạn ạ.
@Nghệ Mạt
#cua