
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)và\(AH\perp BC\)
\(\Rightarrow AH^2=HB.HC\)(Hệ thức lượng)
\(AH^2=25.64\)
\(AH=\sqrt{1600}=40cm\)
Xét \(\Delta ABH\)có\(\widehat{H}=90^o\)
\(\Rightarrow\tan B=\frac{AH}{BH}\)\(=\frac{40}{25}=\frac{8}{5}\)
\(\Rightarrow\widehat{B}\approx58^o\)
Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=90^o\)
\(58^o+\widehat{C}=90^o\)
\(\Rightarrow\widehat{C}\approx90^o-58^o\)
\(\widehat{C}\approx32^o\)

a) (H.a)
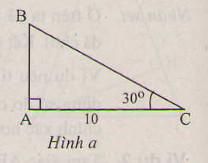
ˆB=90∘−30∘=60∘.B^=90∘−30∘=60∘.
AB=AC⋅tgC=10⋅tg30∘≈5,774(cm)AB=AC⋅tgC=10⋅tg30∘≈5,774(cm)
BC=ACcosC=10cos30∘≈11,547(cm)BC=ACcosC=10cos30∘≈11,547(cm).
b) (H.b)
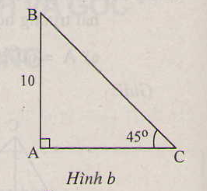
ˆB=90∘−45∘=45∘.B^=90∘−45∘=45∘.
⇒AC=AB=10(cm);⇒AC=AB=10(cm);
BC=ABsinC=10sin45∘≈14,142(cm)BC=ABsinC=10sin45∘≈14,142(cm)
c) (H.c)
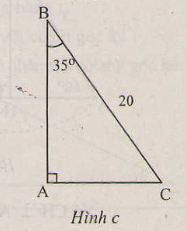
ˆC=90∘−35

a. Ta thấy \(\left(a\sqrt{5}\right)^2=\left(a\sqrt{3}\right)^2+\left(a\sqrt{2}\right)^2\Rightarrow AB^2=BC^2+AC^2\)
\(\Rightarrow\Delta ABC\)vuông tại C
b. \(\sin B=\frac{AC}{AB}=\frac{\sqrt{2}}{\sqrt{5}}=\frac{\sqrt{10}}{5};\cos B=\frac{CB}{AB}=\frac{\sqrt{3}}{\sqrt{5}}=\frac{\sqrt{15}}{5}\)
\(\tan B=\frac{AC}{AB}=\frac{\sqrt{6}}{3};\cot B=\frac{\sqrt{6}}{2}\)
\(\sin A=\cos B=\frac{\sqrt{15}}{5};\cos A=\sin B=\frac{\sqrt{10}}{5}\)
\(\tan A=\cot B=\frac{\sqrt{6}}{2};\cot A=\tan B=\frac{\sqrt{6}}{3}\)

neu ai tra loi dung cho minh trong may tieng nay to k cho1 nink

#)Giải :
a)\(\Delta ABC\)vuông tại A (gt) \(\Rightarrow\widehat{BAD}+\widehat{DAC}=90^o\left(1\right)\)
\(\Delta HAD\)vuông tại H (gt)\(\Rightarrow\widehat{HDA}+\widehat{HAD}=90^o\left(2\right)\)
Vì AD là tia phân giác của \(\widehat{HAC}\Rightarrow\)\(\widehat{HAD}=\widehat{DAC}\left(3\right)\)
Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow\widehat{BAD}=\widehat{DAC}\)
\(\Rightarrow\Delta ABD\)cân tại A
b) Từ cmt \(\Rightarrow AB=BD\)(tính chất của tam giác cân)
Đặt \(AB=BD=x\)
Áp dụng hệ thức lượng trong tam giác vuông ABC
\(\Rightarrow AB^2=HB.HC\)
Hay \(x^2=\left(x-6\right)25\)
\(\Rightarrow x^2-25+150=0\)
\(\Rightarrow\left(x-10\right)\left(x-15\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-10=0\\x-15=0\end{cases}\Rightarrow\orbr{\begin{cases}x=10\\x=15\end{cases}}}\)
Vậy AB = 10 hoặc AB = 15
:v kí hiệu vậy ai biết ở đâu
coi b là cạnh huyền nhé!
Áp dụng Pythagoras cho b = căn 61
Dùng sin cos .-.