Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a/
\(\Leftrightarrow3\left(1-sin^22x\right)+4sin2x-4=0\)
\(\Leftrightarrow-3sin^22x+4sin2x-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=1\\sin2x=\frac{1}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{4}+k\pi\\x=\frac{1}{2}arcsin\left(\frac{1}{3}\right)+k\pi\\x=\frac{\pi}{2}-\frac{1}{2}arcsin\left(\frac{1}{3}\right)+k\pi\end{matrix}\right.\)
b/
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=-1\\cos2x=\frac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=\frac{\pi}{8}+k\pi\\x=-\frac{\pi}{8}+k\pi\end{matrix}\right.\)
f/
\(\Leftrightarrow4\left(1-2sin^2\frac{x}{2}\right)-5sin\frac{x}{2}=1\)
\(\Leftrightarrow8sin^2\frac{x}{2}+5sin\frac{x}{2}-3=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\frac{x}{2}=-1\\sin\frac{x}{2}=\frac{3}{8}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\pi+k4\pi\\x=2arcsin\left(\frac{3}{8}\right)+k4\pi\\x=2\pi-2arcsin\left(\frac{3}{8}\right)+k4\pi\end{matrix}\right.\)
c/
\(\Leftrightarrow\left[{}\begin{matrix}sinx=1\\sinx=-\frac{5}{2}\left(l\right)\end{matrix}\right.\)
\(\Rightarrow x=\frac{\pi}{2}+k2\pi\)
d/
\(\Leftrightarrow2cos^2\frac{x}{2}-1+3cos\frac{x}{2}+2=0\)
\(\Leftrightarrow2cos^2\frac{x}{2}+3cos\frac{x}{2}+1=0\)
\(\Rightarrow\left[{}\begin{matrix}cos\frac{x}{2}=-1\\cos\frac{x}{2}=-\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\frac{x}{2}=\pi+k2\pi\\\frac{x}{2}=\pm\frac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\pi+k4\pi\\x=\pm\frac{4\pi}{3}+k4\pi\end{matrix}\right.\)
a/
\(\Rightarrow\left[{}\begin{matrix}cosx=\frac{1}{2}\\cosx=-\frac{1}{3}\end{matrix}\right.\) (đặt \(cosx=t\) thành pt bậc 2 rồi bấm máy ra nghiệm thôi)
\(\Rightarrow\left[{}\begin{matrix}x=\pm\frac{\pi}{3}+k2\pi\\x=\pm arccos\left(-\frac{1}{3}\right)+k2\pi\end{matrix}\right.\)
b/
\(\Leftrightarrow6\left(1-sin^2x\right)+5sinx-7=0\)
\(\Leftrightarrow-6sin^2x+5sinx-1=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=\frac{1}{2}\\sinx=\frac{1}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{6}+k2\pi\\x=arcsin\left(\frac{1}{3}\right)+k2\pi\\x=\pi-arcsin\left(\frac{1}{3}\right)+k2\pi\end{matrix}\right.\)
Nó là ptlg b2 cơ bản thôi mà, khéo léo biến đổi nó về cùng cos hoặc cùng sin là xét được hết :(
\(\Leftrightarrow1-\sin^2\frac{x}{2}+2\sin\frac{x}{2}+2=0\)
\(\Leftrightarrow\sin^2\frac{x}{2}-2\sin\frac{x}{2}-3=0\)
Ok, giờ đặt sinx=t với t thuộc [-1;1] rồi làm bthg thôi
e.
\(3\left(1-sin^2x\right)-5sinx-1=0\)
\(\Leftrightarrow-3sin^2x-5sinx+2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\frac{1}{3}\\sinx=-2\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=arcsin\left(\frac{1}{3}\right)+k2\pi\\x=\pi-arcsin\left(\frac{1}{3}\right)+k2\pi\end{matrix}\right.\)
f.
\(2\left(2cos^2x-1\right)-cosx+7=0\)
\(\Leftrightarrow4cos^2x-cosx+5=0\)
Phương trình vô nghiệm
g.
\(\Leftrightarrow\sqrt{2}sin\left(4x+\frac{\pi}{4}\right)=2\)
\(\Leftrightarrow sin\left(4x+\frac{\pi}{4}\right)=\sqrt{2}>1\)
Phương trình vô nghiệm
h.
\(\Leftrightarrow\frac{\sqrt{3}}{2}sinx-\frac{1}{2}cosx=\frac{1}{2}\)
\(\Leftrightarrow sin\left(x-\frac{\pi}{6}\right)=\frac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\frac{\pi}{6}=\frac{\pi}{6}+k2\pi\\x-\frac{\pi}{6}=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{3}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)
3) 2sin^2 x - 3sinx + 1 = 0
Đặt t = sin x
(*) <=> 2t^2 - 3t + 1 = 0
<=> t = 1 (nhận) or t = 1/2 (nhận)
.Vs t = 1 => sinx = 1
<=> x = π/2 + k2π (k thuộc Z) (nhận)
.Vs t = 1/2 => sinx = 1/2
<=> sinx = sin π/6
<=> x = π/6 + k2π (k thuộc Z) (nhận)
Vậy ...
2) cos^2 x + cosx = 0
Đặt t = cosx
(*) <=> t^2 + t =0 <=> t = 0 (n) or t = -1 (n)
. Vs t = 0 => cosx = 0 <=> x = π/2 + kπ (loại)
.Vs t = -1 => cosx = -1 <=> x = π + k2π (nhận)
Vậy ...
1) (sin3x)/cosx + 1 = 0
ĐK: cosx + 1 ≠ 0 <=> cosx ≠ -1 <=> x ≠ π + k2π
<=> sin3x = 0
<=> 3x = kπ
<=> x = 1/3 kπ (k thuộc Z) (n)
Vậy ...
2sin2x + sinx.cosx – 3cos2x = 0 (1)
+ Xét cos x = 0 ⇒ sin2x = 1 – cos2x = 1
Phương trình (1) trở thành: 2 = 0 (loại)
+ Xét cos x ≠ 0, chia cả hai vế của (1) cho cos2x ta được:
Vậy phương trình có tập nghiệm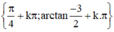
(k ∈ Z)