
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




1/ \(x^3-7x+6=0\)
\(\Leftrightarrow x^3+3x^2-3x^2-9x+2x+6=0\)
\(\Leftrightarrow x^2\left(x+3\right)-3x\left(x+3\right)+2\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^2-3x+2\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^2-x-2x+2\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left[x\left(x-1\right)+2\left(x-1\right)\right]=0\)
\(\Leftrightarrow\left(x+3\right)\left(x-1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\)\(x+3=0\)
hoặc \(x-1=0\)
hoặc \(x+2=0\)
\(\Leftrightarrow\)\(x=-3\)
hoặc \(x=1\)
hoặc \(x=-2\)
Vậy tập nghiệm của phương trình là : \(S=\left\{-3;1;-2\right\}\)
2/ \(x^3-6x^2-x+30\)
\(\Leftrightarrow x^3+2x^2-8x^2-16x+15x+30=0\)
\(\Leftrightarrow x^2\left(x+2\right)-8x\left(x+2\right)+15\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-8x+15\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-3x-5x+15\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left[x\left(x-3\right)-5\left(x-3\right)\right]=0\)
\(\Leftrightarrow\left(x+2\right)\left(x-3\right)\left(x-5\right)=0\)
\(\Leftrightarrow\)\(x+2=0\)
hoặc \(x-3=0\)
hoặc \(x-5=0\)
\(\Leftrightarrow\)\(x=-2\)
hoặc \(x=3\)
hoặc \(x=5\)
Vậy tập nghiệm của phương trình là :\(S=\left\{-2;3;5\right\}\)
3/ \(x^3-9x^2+6x+16=0\)
\(\Leftrightarrow x^3+x^2-10x^2-10x+16x+16=0\)
\(\Leftrightarrow x^2\left(x+1\right)-10x\left(x+1\right)+16\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-10x+16\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-8x-2x+16\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left[x\left(x-8\right)-2\left(x-8\right)\right]=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-8\right)\left(x-2\right)=0\)
\(\Leftrightarrow\)\(x+1=0\)
hoặc \(x-8=0\)
hoặc \(x-2=0\)
\(\Leftrightarrow\)\(x=-1\)
hoặc \(x=8\)
hoặc \(x=2\)
Vậy tập nghiệm của phương trình là :\(S=\left\{-1;8;2\right\}\)
4/ Đề bài sai ! Sửa lại nhé :
\(2x^3-x^2+5x+3=0\)
\(\Leftrightarrow2x^3+x^2-2x^2-x+6x+3=0\)
\(\Leftrightarrow x^2\left(2x+1\right)-x\left(2x+1\right)+3\left(2x-1\right)=0\)
\(\Leftrightarrow\left(2x+1\right)\left(x^2-x+3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x+1=0\\x^2-x+3=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-\frac{1}{2}\left(tm\right)\\\left(x-\frac{1}{2}\right)^2+\frac{11}{4}=0\left(ktm\right)\end{cases}}\)
Vậy tập nghiệm của phương trình là : \(S=\left\{-\frac{1}{2}\right\}\)

a/. x3 - 9x2 +27x - 19 = 0
<=> (x3 - 3.x2 .3 + 3.32 .x - 33) + 8 = 0
<=> (x - 3)3 + 8 = 0
<=> (x - 3 + 2) [(x - 3)2 - 2(x-3) +4] = 0
<=> (x -1)(x2 - 6x+ 9 -2x +6 +4) =0
<=> (x - 1)(x2 - 8x + 19) = 0
<=> x - 1 = 0 => x = 1
Vậy S = {1}
Xem lại đề câu b nha bạn?
c/. x3 + 1 -7x -7 =0
<=> (x3 + 1) -7(x+1)=0
<=> (x+1)(x2-x+1) -7(x+1)=0
<=> (x+1)(x2-x+1-7)=0
<=> x + 1 = 0 hay x2 -x - 6 = 0
<=> x = -1 hay (x2 - 3x) + (2x - 6) = 0
<=> x(x - 3) +2(x-3) = 0
<=> (x - 3)(x+2) = 0
<=> x = -1 hay x = 3 hay x = -2
Vậy S = {-1;3;-2}
X3 - X2-8X2+8X+19X-19=0
<=>X2(X-1)-8X(X-1)+19(X-1)=0
<=>(X-1)(X2-8X+19)=0
vi X2-8X+19=(X-4)2+3>3

a) \(\left(x+2\right)^2-3x^2=-12\)
\(\Leftrightarrow x^2+4x+4-3x^2+12=0\)
\(\Leftrightarrow-2x^2+4x+16=0\)
\(\Leftrightarrow-2\left(x^2-2x-8\right)=0\)
\(\Leftrightarrow x^2-2x-8=0\)
\(\Leftrightarrow x^2-4x+2x-8=0\)
\(\Leftrightarrow x\left(x-4\right)+2\left(x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=4\\x=-2\end{cases}}\)
Vậy....
b) \(3x^2-2x-1=0\)
\(\Leftrightarrow3x^2-3x+x-1=0\)
\(\Leftrightarrow3x\left(x-1\right)+\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\\x=\frac{-1}{3}\end{cases}}\)
Vậy....
c) \(\frac{7x-3}{x-1}=\frac{2}{3}\)ĐKXĐ : \(x\ne1\)
\(\Rightarrow3\left(7x-3\right)=2\left(x-1\right)\)
\(\Leftrightarrow21x-9=2x-2\)
\(\Leftrightarrow21x-2x=-2+9\)
\(\Leftrightarrow19x=7\)
\(\Leftrightarrow x=\frac{7}{19}\)( thỏa mãn ĐKXĐ )
Vậy....
d) \(\frac{3x-4}{x^2}-\frac{1}{x+1}=0\)
\(\Leftrightarrow\frac{3x-4}{x^2}=\frac{1}{x+1}\)
\(\Rightarrow\left(x+1\right)\left(3x-4\right)=x^2\)
\(\Leftrightarrow3x^2-x-4-x^2=0\)
\(\Leftrightarrow2x^2-x-4=0\)
....
Câu 1
Một ô tô đy từ A đến B với vận tốc 35km/h. Khi từ B về A ô tô đy với vận tốc 42km/h vì vậy thời gian về ít hơn thời gian đy là nửa giờ. Tính độ dài quãng đường AB.
Câu 2
Số học sinh của lớp 8a hơn số học sinh của lớp 8b là 5 bạn. Nếu chuyển 10 bạn từ lớp 8a sang lớp 8b thì số học sinh của lớp 8b sẽ gấp rưỡi số học sinh của lớp 8a. Tính số học sinh lúc đầu của mỗi lớp.

\(a)x^3-\frac{x}{49}=0\)
\(\Leftrightarrow x\left(x^2-\frac{1}{7^2}\right)=0\)
\(\Leftrightarrow x=0\)Hoặc \(x^2-\frac{1}{7^2}=0\)
TH1: \(x\left(x^2-\frac{1}{7^2}\right)=0\\ x=\frac{0}{x^2-\frac{1}{7^2}}\\ \Leftrightarrow x=0\)
TH2: \(x\left(x^2-\frac{1}{7^2}\right)=0\\ x^2-\frac{1}{7^2}=\frac{0}{x}\\ x^2=0+\frac{1}{7^2}\\ x^2=\frac{1}{7^2}\\ x^2=\left(\frac{1}{7}\right)^2\\ \Leftrightarrow x=\frac{1}{7}\)
Vậy \(x=0\)Hoặc \(x=\frac{1}{7}\)
a) x3 - x/49 = 0
<=> x(x2 - 1/49) = 0
<=> x = 0 hoặc x2 - 1/49 = 0
<=> x = 0 hoặc x = +1/7
b) x2 - 7x + 12 = 0
<=> (x - 3)(x - 4) = 0
<=> x - 3 = 0 hoặc x - 4 = 0
<=> x = 3 hoặc x = 4
c) 4x2 - 3x - 1 = 0
<=> 4x2 + x - 4x - 1 = 0
<=> x(4x + 1) - (4x + 1) = 0
<=> (4x + 1)(x - 1) = 0
<=> 4x + 1 = 0 hoặc x - 1 = 0
<=> x = -1/4 hoặc x = 1
d) x3 - 2x - 4 = 0
<=> (x2 + 2x + 2)(x - 2) = 0
vì x2 + 2x + 2 khác 0 nên:
<=> x - 2 = 0
<=> x = 2
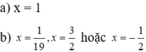
Bài làm
27x2( x + 3 ) - 12( x2 + 3x ) = 0
<=> 27x2( x + 3 ) - 12x( x + 3 ) = 0
<=> x( 27x - 12 )( x + 3 ) = 0
<=> x = 0 hoặc \(\orbr{\begin{cases}27x-12=0\\x+3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{12}{27}\\x=-3\end{cases}}}\)
Vậy S = { 0; 12/27; -3 }
# Học tốt #
27x2 ( x + 3 ) - 12x ( x + 3) = 0
3x ( x + 3 ) ( 9x - 4 ) = 0
=>\(\hept{\begin{cases}3x=0\\x+3=0\\9x-4=0\end{cases}}\Rightarrow\hept{\begin{cases}x=0\\x=-3\\x=\frac{4}{9}\end{cases}}\)
Vậy ngiệm của đa thức là: \(S=\left(-3;\frac{4}{9};0\right)\)