
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

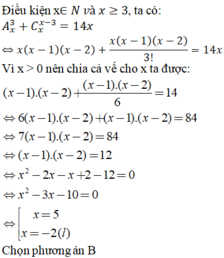

gợi ý: a)chia 2 vế cho căn 5
đặt \(\frac{1}{\sqrt{5}}=cosa\Rightarrow\frac{2}{\sqrt{5}}=sina\)
khi đó pt <=>sin(x-a)=\(\frac{3}{\sqrt{5}}>1\)
->vô nghiệm
bn giải thích cho mk chỗ này được ko : \(\frac{1}{\sqrt{5}}=\cos a\Rightarrow\frac{2}{\sqrt{5}}=\sin a\)

a) cosx - √3sinx = √2 ⇔ cosx - tan![]() sinx = √2
sinx = √2
⇔ cos![]() cosx - sin
cosx - sin![]() sinx = √2cos
sinx = √2cos![]() ⇔ cos(x +
⇔ cos(x + ![]() ) =
) = ![]()
⇔ 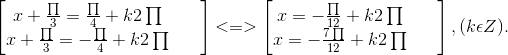
b) 3sin3x - 4cos3x = 5 ⇔ ![]() sin3x -
sin3x - ![]() cos3x = 1.
cos3x = 1.
Đặt α = arccos![]() thì phương trình trở thành
thì phương trình trở thành
cosαsin3x - sinαcos3x = 1 ⇔ sin(3x - α) = 1 ⇔ 3x - α = ![]() + k2π
+ k2π
⇔ x = ![]() , k ∈ Z (trong đó α = arccos
, k ∈ Z (trong đó α = arccos![]() ).
).

a) Dễ thấy cosx = 0 không thỏa mãn phương trình đã cho nên chiaw phương trình cho cos2x ta được phương trình tương đương 2tan2x + tanx - 3 = 0.
Đặt t = tanx thì phương trình này trở thành
2t2 + t - 3 = 0 ⇔ t ∈ {1 ; ![]() }.
}.
Vậy ![]()
b) Thay 2 = 2(sin2x + cos2x), phương trình đã cho trở thành
3sin2x - 4sinxcosx + 5cos2x = 2sin2x + 2cos2x
⇔ sin2x - 4sinxcosx + 3cos2x = 0
⇔ tan2x - 4tanx + 3 = 0
⇔ ![]()
⇔ x = ![]() + kπ ; x = arctan3 + kπ, k ∈ Z.
+ kπ ; x = arctan3 + kπ, k ∈ Z.
c) Thay sin2x = 2sinxcosx ; ![]() =
= ![]() (sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
(sin2x + cos2x) vào phương trình đã cho và rút gọn ta được phương trình tương đương
![]() sin2x + 2sinxcosx -
sin2x + 2sinxcosx - ![]() cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔
cos2x = 0 ⇔ tan2x + 4tanx - 5 = 0 ⇔ ![]()
⇔ x = ![]() + kπ ; x = arctan(-5) + kπ, k ∈ Z.
+ kπ ; x = arctan(-5) + kπ, k ∈ Z.
d) 2cos2x - 3√3sin2x - 4sin2x = -4
⇔ 2cos2x - 3√3sin2x + 4 - 4sin2x = 0
⇔ 6cos2x - 6√3sinxcosx = 0 ⇔ cosx(cosx - √3sinx) = 0
⇔ 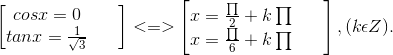

\(sin\left(x-\frac{\pi}{3}\right)=1\Rightarrow x-\frac{\pi}{3}=\frac{\pi}{2}+k2\pi\Rightarrow x=\frac{5\pi}{6}+k2\pi\)

\(sin\left(\frac{2x}{3}-60^0\right)=0\Rightarrow\frac{2x}{3}-60^0=k.180^0\)
\(\Rightarrow\frac{2x}{3}=60^0+k180^0\Rightarrow x=90^0+k270^0\)
Tất cả các đáp án đều sai, đề bài cho đơn vị độ nhưng đáp án lại cho đơn vị biểu diễn là radian

3.
\(x-2y+1=0\Leftrightarrow y=\frac{1}{2}x+\frac{1}{2}\)
\(y'=\frac{2}{\left(x+1\right)^2}\Rightarrow\frac{2}{\left(x+1\right)^2}=\frac{1}{2}\)
\(\Rightarrow\left(x+1\right)^2=4\Rightarrow\left[{}\begin{matrix}x=1\Rightarrow y=1\\x=-3\Rightarrow y=3\end{matrix}\right.\)
Có 2 tiếp tuyến: \(\left[{}\begin{matrix}y=\frac{1}{2}\left(x-1\right)+1\\y=\frac{1}{2}\left(x+3\right)+3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}y=\frac{1}{2}x+\frac{1}{2}\left(l\right)\\y=\frac{1}{2}x+\frac{9}{2}\end{matrix}\right.\)
4.
\(\lim\limits\frac{\sqrt{2n^2+1}-3n}{n+2}=\lim\limits\frac{\sqrt{2+\frac{1}{n^2}}-3}{1+\frac{2}{n}}=\sqrt{2}-3\)
\(\Rightarrow\left\{{}\begin{matrix}a=2\\b=3\end{matrix}\right.\)
5.
\(\lim\limits_{x\rightarrow a}\frac{2\left(x^2-a^2\right)+a\left(a+1\right)-\left(a+1\right)x}{\left(x-a\right)\left(x+a\right)}=\lim\limits_{x\rightarrow a}\frac{\left(x-a\right)\left(2x+2a\right)-\left(a+1\right)\left(x-a\right)}{\left(x-a\right)\left(x+a\right)}\)
\(=\lim\limits_{x\rightarrow a}\frac{\left(x-a\right)\left(2x+a-1\right)}{\left(x-a\right)\left(x+a\right)}=\lim\limits_{x\rightarrow a}\frac{2x+a-1}{x+a}=\frac{3a-1}{2a}\)
1.
\(f'\left(x\right)=-3x^2+6mx-12=3\left(-x^2+2mx-4\right)=3g\left(x\right)\)
Để \(f'\left(x\right)\le0\) \(\forall x\in R\) \(\Leftrightarrow g\left(x\right)\le0;\forall x\in R\)
\(\Leftrightarrow\Delta'=m^2-4\le0\Rightarrow-2\le m\le2\)
\(\Rightarrow m=\left\{-1;0;1;2\right\}\)
2.
\(f'\left(x\right)=\frac{m^2-20}{\left(2x+m\right)^2}\)
Để \(f'\left(x\right)< 0;\forall x\in\left(0;2\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2-20< 0\\\left[{}\begin{matrix}m>0\\m< -4\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-\sqrt{20}< m< \sqrt{20}\\\left[{}\begin{matrix}m>0\\m< -4\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow m=\left\{1;2;3;4\right\}\)