Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

d) Điều kiện \(\begin{cases}x\ne0\\\log_2\left|x\right|\ge0\end{cases}\)\(\Leftrightarrow\left|x\right|\ge\)1
Phương trình đã cho tương đương với :
\(\log_2\left|x\right|^{\frac{1}{2}}-4\sqrt{\log_{2^2}\left|x\right|}-5=0\)
\(\Leftrightarrow\frac{1}{2}\log_2\left|x\right|-4\sqrt{\frac{1}{4}\log_2\left|x\right|}-5=0\)
Đặt \(t=\sqrt{\frac{1}{2}\log_2\left|x\right|}\) \(\left(t\ge0\right)\) thì phương trình trở thành :
\(t^2-4t-5=0\) hay t=-1 V t=5
Do \(t\ge0\) nên t=5
\(\Rightarrow\frac{1}{2}\log_2\left|x\right|=25\Leftrightarrow\log_2\left|x\right|=50\Leftrightarrow\left|x\right|=2^{50}\) Thỏa mãn
Vậy \(x=\pm2^{50}\) là nghiệm của phương trình
c) Điều kiện x>0. Phương trình đã cho tương đương với :
\(x^{lg^2x^2-3lgx-\frac{9}{2}}=\left(10^{lgx}\right)^{-2}\)
\(\Leftrightarrow lg^2x^2-3lgx-\frac{9}{2}=-2\)
\(\Leftrightarrow8lg^2x-6lgx-5=0\)
Đặt \(t=lgx\left(t\in R\right)\) thì phương trình trở thành
\(8t^2-6t-5=0\) hay\(t=-\frac{1}{2}\) V \(t=\frac{5}{4}\)
Với \(t=-\frac{1}{2}\) thì \(lgx=-\frac{1}{2}\Leftrightarrow x=\frac{1}{\sqrt{10}}\)
Với \(t=\frac{5}{4}\) thì \(lgx=\frac{5}{4}\Leftrightarrow x=\sqrt[4]{10^5}\)
Vậy phương trình đã cho có nghiệm \(x=\sqrt[4]{10^5}\) và \(x=\frac{1}{\sqrt{10}}\)

d) Điều kiện x>0. Áp dụng công thức đổi cơ số, ta có :
\(\log_2x+\log_3x+\log_4x=\log_{20}x\)
\(\Leftrightarrow\log_2x+\frac{\log_2x}{\log_23}+\frac{\log_2x}{\log_24}=\frac{\log_2x}{\log_220}\)
\(\Leftrightarrow\log_2x\left(1+\frac{1}{\log_23}+\frac{1}{2}+\frac{1}{\log_220}\right)=0\)
\(\Leftrightarrow\log_2x\left(\frac{3}{2}+\log_22-\log_{20}2\right)=0\)
Ta có \(\frac{3}{2}+\log_22-\log_{20}2>\frac{3}{2}+0-1>0\)
Do đó, từ phương trình trên, ta phải có \(\log_2x=0\) hay \(x=2^0=1\)
Vậy nghiệm duy nhất của phương trình là \(x=1\)
c) Điều kiện x>0, đưa về cùng cơ số 5, ta có :
\(\log_5x^3+3\log_{25}x+\log_{\sqrt{25}}\sqrt{x^3}=\frac{11}{2}\)
\(\Leftrightarrow3\log_5x+3\log_{5^2}x+\log_{5^{\frac{3}{2}}}x^{\frac{3}{2}}=\frac{11}{2}\)
\(\Leftrightarrow3\log_5x+3\frac{1}{2}\log_5x+\frac{3}{2}.\frac{2}{3}\log_5x=\frac{11}{2}\)
\(\Leftrightarrow\frac{11}{2}\log_5x=\frac{11}{2}\)
\(\Leftrightarrow\log_5x=1\)
\(\Leftrightarrow x=5^1=5\) thỏa mãn
Vậy phương trình chỉ có 1 nghiệ duy nhất \(x=5\)

Câu 1:
Đặt \(\sqrt{lnx+1}=t\Rightarrow lnx=t^2-1\Rightarrow\frac{dx}{x}=2tdt\)
\(\Rightarrow I=\int3t.2t.dt=6\int t^2dt=2t^3+C\)
\(=2\sqrt{\left(lnx+1\right)^3}+C=2\left(lnx+1\right)\sqrt{lnx+1}+C\)
\(=ln\left(x.e\right)^2\sqrt{ln\left(x.e\right)+0}\Rightarrow a=2;b=0\)
Câu 2:
\(\int\limits^b_ax^{-\frac{1}{2}}dx=2x^{\frac{1}{2}}|^b_a=2\left(\sqrt{b}-\sqrt{a}\right)=2\Rightarrow\sqrt{b}-\sqrt{a}=1\)
Ta có hệ: \(\left\{{}\begin{matrix}\sqrt{b}-\sqrt{a}=1\\a^2+b^2=17\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=4\\a=1\end{matrix}\right.\) (lưu ý loại cặp nghiệm âm do \(\frac{1}{\sqrt{x}}\) chỉ xác định trên miền (a;b) dương)
Câu 4:
\(\int\frac{3x+a}{x^2+4}dx=\frac{3}{2}\int\frac{2x}{x^2+4}dx+a\int\frac{1}{x^2+4}dx\)
\(=\frac{3}{2}ln\left(x^2+4\right)+\frac{a}{2}arctan\left(\frac{x}{2}\right)+C\)
\(\Rightarrow a=2\)
\(\Rightarrow I=\int\limits^{\frac{e}{4}}_1ln\left(x\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=lnx\\dv=dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\frac{1}{x}dx\\v=x\end{matrix}\right.\)
\(\Rightarrow I=x.lnx|^{\frac{e}{4}}_1-\int\limits^{\frac{e}{4}}_1dx=\frac{e}{4}.ln\left(\frac{e}{4}\right)-\frac{e}{4}+1=-\frac{ln\left(2^e\right)}{2}+1\)
Câu 5:
\(f'\left(x\right)=\int f''\left(x\right)dx=-\frac{1}{4}\int x^{-\frac{3}{2}}dx=\frac{1}{2\sqrt{x}}+C\)
\(f'\left(2\right)=\frac{1}{2\sqrt{2}}+C=2+\frac{1}{2\sqrt{2}}\Rightarrow C=2\)
\(\Rightarrow f'\left(x\right)=\frac{1}{2\sqrt{x}}+2\)
\(\Rightarrow f\left(x\right)=\int f'\left(x\right)dx=\int\left(\frac{1}{2\sqrt{x}}+2\right)dx=\sqrt{x}+2x+C_1\)
\(f\left(4\right)=\sqrt{4}+2.4+C_1=10\Rightarrow C_1=0\)
\(\Rightarrow f\left(x\right)=2x+\sqrt{x}\)
\(\Rightarrow F\left(x\right)=\int f\left(x\right)dx=\int\left(2x+\sqrt{x}\right)dx=x^2+\frac{2}{3}\sqrt{x^3}+C_2\)
\(F\left(1\right)=1+\frac{2}{3}+C_2=1+\frac{2}{3}\Rightarrow C_2=0\)
\(\Rightarrow F\left(x\right)=x^2+\frac{2}{3}\sqrt{x^3}\Rightarrow\int\limits^1_0\left(x^2+\frac{2}{3}\sqrt{x^3}\right)dx=\frac{3}{5}\)

1) Đặt \(2+lnx=t\Leftrightarrow x=e^{t-2}\Rightarrow dx=e^{t-2}dt\)
\(I_1=\int\left(\frac{t-2}{t}\right)^2\cdot e^{t-2}\cdot dt=\int\left(1-\frac{4}{t}+\frac{4}{t^2}\right)e^{t-2}dt\\ =\int e^{t-2}dt-4\int\frac{e^{t-2}}{t}dt+4\int\frac{e^{t-2}}{t^2}dt\)
Có:
\(4\int\frac{e^{t-2}}{t^2}dt=-4\int e^{t-2}\cdot d\left(\frac{1}{t}\right)=-\frac{4\cdot e^{t-2}}{t}+4\int\frac{e^{t-2}}{t}dt\\ \Leftrightarrow4\int\frac{e^{t-2}}{t^2}dt-4\int\frac{e^{t-2}}{t^{ }}dt=-\frac{4\cdot e^{t-2}}{t}\)
Vậy \(I_1=\int e^{t-2}dt-\frac{4\cdot e^{t-2}}{t}=e^{t-2}-\frac{4e^{t-2}}{t}+C\)
3) Đặt \(t=\sqrt{1+\sqrt[3]{x^2}}\Rightarrow t^2-1=\sqrt[3]{x^2}\Leftrightarrow x^2=\left(t^2-1\right)^3\)
\(d\left(x^2\right)=d\left[\left(t^2-1\right)^3\right]\Leftrightarrow2x\cdot dx=6t\left(t^2-1\right)^2\cdot dt\)
\(I_3=\int\frac{3t\left(t^2-1\right)^2}{t}dt=3\int\left(t^4-2t^2+1\right)dt=...\)

a) Đặt t = 13x > 0 ta được phương trình:
13t2 – t – 12 = 0 ⇔ (t – 1)(13t + 12) = 0
⇔ t = 1 ⇔ 13x = 1 ⇔ x = 0
b)
Chia cả hai vế phương trình cho 9x ta được phương trình tương đương
(1+(23)x)(1+3.(23)x)=8.(23)x(1+(23)x)(1+3.(23)x)=8.(23)x
Đặt t=(23)xt=(23)x (t > 0) , ta được phương trình:
(1 + t)(1 + 3t) = 8t ⇔ 3t2 – 4t + 1 = 0 ⇔ t∈{13,1}t∈{13,1}
Với t=13t=13 ta được nghiệm x=log2313x=log2313
Với t = 1 ta được nghiệm x = 0
c) Điều kiện: x > 2
Vì nên phương trình đã cho tương đương với:
[log3(x−2)=0log5x=1⇔[x=3x=5[log3(x−2)=0log5x=1⇔[x=3x=5
d) Điều kiện: x > 0
log22x – 5log2x + 6 = 0
⇔(log2x – 2)(log2x – 3) = 0
⇔ x ∈ {4, 8}

d) Đưa 2 vế về cùng cơ số 2, ta được
\(2^{-3}.2^{4x-6}=\left(2^{\frac{-5}{2}}\right)^x\) hay \(2^{4x-9}=2^{\frac{5}{2}x}\)
Do đó :
\(4x-9=\frac{5}{2}x\Leftrightarrow\frac{3}{2}x=9\Leftrightarrow x=6\)
Vậy phương trình đã cho chỉ có 1 nghiệm x=6
c) Phương trình đã cho tương đương với :
\(\frac{1}{4}.4^x+16.4^x=10\Leftrightarrow\frac{33}{2}.4^x=10\Leftrightarrow4^x=\frac{20}{33}\Leftrightarrow x=\log_4\frac{20}{33}\)
Vậy nghiệm của phương trình là \(x=\log_4\frac{20}{33}\)

14.
\(log_aa^2b^4=log_aa^2+log_ab^4=2+4log_ab=2+4p\)
15.
\(\frac{1}{2}log_ab+\frac{1}{2}log_ba=1\)
\(\Leftrightarrow log_ab+\frac{1}{log_ab}=2\)
\(\Leftrightarrow log_a^2b-2log_ab+1=0\)
\(\Leftrightarrow\left(log_ab-1\right)^2=0\)
\(\Rightarrow log_ab=1\Rightarrow a=b\)
16.
\(2^a=3\Rightarrow log_32^a=1\Rightarrow log_32=\frac{1}{a}\)
\(log_3\sqrt[3]{16}=log_32^{\frac{4}{3}}=\frac{4}{3}log_32=\frac{4}{3a}\)
11.
\(\Leftrightarrow1>\left(2+\sqrt{3}\right)^x\left(2+\sqrt{3}\right)^{x+2}\)
\(\Leftrightarrow\left(2+\sqrt{3}\right)^{2x+2}< 1\)
\(\Leftrightarrow2x+2< 0\Rightarrow x< -1\)
\(\Rightarrow\) có \(-2+2020+1=2019\) nghiệm
12.
\(\Leftrightarrow\left\{{}\begin{matrix}x-2>0\\0< log_3\left(x-2\right)< 1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>2\\1< x-2< 3\end{matrix}\right.\)
\(\Rightarrow3< x< 5\Rightarrow b-a=2\)
13.
\(4^x=t>0\Rightarrow t^2-5t+4\ge0\)
\(\Rightarrow\left[{}\begin{matrix}t\le1\\t\ge4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}4^x\le1\\4^x\ge4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x\le0\\x\ge1\end{matrix}\right.\)
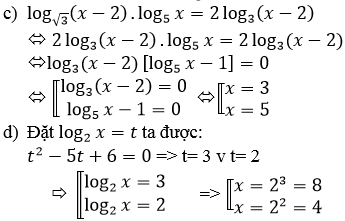
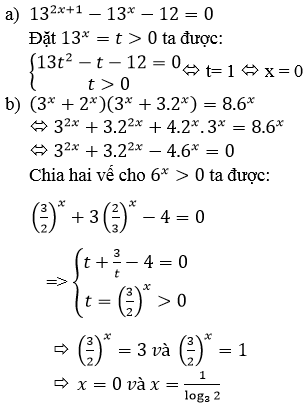
a) Điều kiện \(x-4>0\Leftrightarrow x>4\)
Đặt \(f\left(x\right)=lg\left(x-4\right),g\left(x\right)=5-x\)
Phương trình đã cho trở thành
\(f\left(x\right)=g\left(x\right)\)
Ta có \(f\left(x\right)\) đồng biến trên \(\left(4;+\infty\right)\) và \(g\left(x\right)\) nghịch biến trên R
Hơn nữa \(f\left(5\right)=g\left(5\right)\) do đó \(x=5\) là nghiệm duy nhất của phương trình
b) Dễ thấy \(x=\sqrt{2}\) là nghiệm của phương trình.
Nếu \(x>\sqrt{2}\) thì \(x^x>\left(\sqrt{2}\right)^x>\left(\sqrt{2}\right)^{\sqrt{2}}\)
Tương tự \(x<\sqrt{2}\) . Vậy \(x=\sqrt{2}\) là nghiệm duy nhất