
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4x-x-18=0
3x-18=0
3x=0+18 = 18
=> 3x = 18:3=6
vậy x sẽ là 6
3x-18=0
3x=0+18
3x=18
x=18:3
x=6
Vậy x=6
mk ko bt giải phg trình nên giải = cách này

\(x^4+4x^3+5x^2-4x+4=0\)
\(\Leftrightarrow x^4+4x^3+4x^2+x^2-4x+4=0\)
\(\Leftrightarrow x^2\left(x+2\right)^2+\left(x-2\right)^2=0\)
Vì \(x^2\left(x+2\right)^2\ge0\forall x;\left(x-2^2\right)\ge0\forall x\)
\(\Rightarrow x^2\left(x+2\right)^2+\left(x-2\right)^2\ge0\)
Mà \(x^2\left(x+2\right)^2+\left(x-2\right)^2=0\)
\(\Rightarrow\hept{\begin{cases}x\left(x+2\right)=0\\x-2=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=0;x=-2\\x=2\end{cases}}\)
Mà ko cùng một lúc tồn tại 2 giá trị của x
\(\Rightarrow\)Phương trình vô nghiệm
Vậy ...

Bổ đề a^3+b^3+c^3-3abc= 0
<=> (a+b+c)[a^2+b^2+c^2-ab-bc-ca]=0
<=> 1/2 .(a+b+c)[(a-b)^2+(b-c)^2+(c-a)^2]=0
<=> a+b+c=0 hoặc a=b=c
Đặt u =x^2-3 , v= - (4x+6 )
Ta có u^3+v^3 +216 = 18.u.v
<=> u^3+v^3+6^3 - 3.6.uv=0
Áp dụng bổ đề
=> u=v=3 hoặc u+v+3=0
*TH1: u=v=3 => x^2-3=3 và 4x+6=-3 ( vô lý)
*TH2 : u+v+3=0 <=> x^2-3-(4x+6)+3=0 <=> x^2-4x-6=0
=> x=2+√10 hay x=2-√10

Ta có: 4x - x - 18 = 0 ⇔ 3x - 18 = 0 ⇔ 3x = 18 ⇔ x = 18/3 = 6.
Vậy phương trình có nghiệm là x = 6.
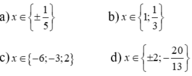
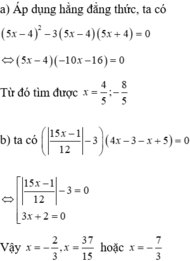
\(\Leftrightarrow4x^3+8x^2-12x^2-24x+9x+18=0\)
\(\Leftrightarrow\left(x+2\right)\left(4x^2-12x+9\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(2x-3\right)^2=0\)
=>x=3/2 hoặc x=-2
4x^3-4x^2-15x+18=0
<=> 4x^3 +8x^2-12x^2-24x+9x+18=0
<=> 4x^2(x+2)-12x(x+2)+9(x+2)=0
<=> (x+2).(4x^2-12x+9)=0
<=> (x+2).(2x-3)^2=0
<=> x+2=0
(2x-3)^2=0
<=> x=-2
x=3/2