Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) 7x - 35 = 0
<=> 7x = 0 + 35
<=> 7x = 35
<=> x = 5
b) 4x - x - 18 = 0
<=> 3x - 18 = 0
<=> 3x = 0 + 18
<=> 3x = 18
<=> x = 5
c) x - 6 = 8 - x
<=> x - 6 + x = 8
<=> 2x - 6 = 8
<=> 2x = 8 + 6
<=> 2x = 14
<=> x = 7
d) 48 - 5x = 39 - 2x
<=> 48 - 5x + 2x = 39
<=> 48 - 3x = 39
<=> -3x = 39 - 48
<=> -3x = -9
<=> x = 3

1, |x-7|=x-7
x-7= -( x-7 ) hoặc x-7= x-7
tự giải 2 trường hợp :v

a) ĐKXĐ: \(x\notin\left\{-1;0\right\}\)
Ta có: \(\dfrac{x+3}{x+1}+\dfrac{x-2}{x}=2\)
\(\Leftrightarrow\dfrac{x\left(x+3\right)}{x\left(x+1\right)}+\dfrac{\left(x+1\right)\left(x-2\right)}{x\left(x+1\right)}=\dfrac{2x\left(x+1\right)}{x\left(x+1\right)}\)
Suy ra: \(x^2+3x+x^2-3x+2=2x^2+2x\)
\(\Leftrightarrow2x^2+2-2x^2-2x=0\)
\(\Leftrightarrow-2x+2=0\)
\(\Leftrightarrow-2x=-2\)
hay x=1(nhận)
Vậy: S={1}
b) ĐKXĐ: \(x\notin\left\{-7;\dfrac{3}{2}\right\}\)
Ta có: \(\dfrac{3x-2}{x+7}=\dfrac{6x+1}{2x-3}\)
\(\Leftrightarrow\left(3x-2\right)\left(2x-3\right)=\left(6x+1\right)\left(x+7\right)\)
\(\Leftrightarrow6x^2-9x-4x+6=6x^2+42x+x+7\)
\(\Leftrightarrow6x^2-13x+6-6x^2-43x-7=0\)
\(\Leftrightarrow-56x-1=0\)
\(\Leftrightarrow-56x=1\)
hay \(x=-\dfrac{1}{56}\)(nhận)
Vậy: \(S=\left\{-\dfrac{1}{56}\right\}\)
c) ĐKXĐ: \(x\ne-\dfrac{2}{3}\)
Ta có: \(\dfrac{5}{3x+2}=2x-1\)
\(\Leftrightarrow5=\left(3x+2\right)\left(2x-1\right)\)
\(\Leftrightarrow6x^2-3x+4x-2-5=0\)
\(\Leftrightarrow6x^2+x-7=0\)
\(\Leftrightarrow6x^2-6x+7x-7=0\)
\(\Leftrightarrow6x\left(x-1\right)+7\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(6x+7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\6x+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\6x=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(nhận\right)\\x=-\dfrac{7}{6}\left(nhận\right)\end{matrix}\right.\)
Vậy: \(S=\left\{1;-\dfrac{7}{6}\right\}\)
d) ĐKXĐ: \(x\ne\dfrac{2}{7}\)
Ta có: \(\left(2x+3\right)\cdot\left(\dfrac{3x+8}{2-7x}+1\right)=\left(x-5\right)\left(\dfrac{3x+8}{2-7x}+1\right)\)
\(\Leftrightarrow\left(2x+3\right)\cdot\left(\dfrac{3x+8+2-7x}{2-7x}\right)-\left(x-5\right)\left(\dfrac{3x+8+2-7x}{2-7x}\right)=0\)
\(\Leftrightarrow\left(2x+3-x+5\right)\cdot\dfrac{-4x+6}{2-7x}=0\)
\(\Leftrightarrow\left(x+8\right)\cdot\left(-4x+6\right)=0\)(Vì \(2-7x\ne0\forall x\) thỏa mãn ĐKXĐ)
\(\Leftrightarrow\left[{}\begin{matrix}x+8=0\\-4x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-8\\-4x=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-8\left(nhận\right)\\x=\dfrac{3}{2}\left(nhận\right)\end{matrix}\right.\)
Vậy: \(S=\left\{-8;\dfrac{3}{2}\right\}\)

a. 3(x-2)-10=5(2x + 1)
<=> 3x - 6 - 10 = 10x + 5
<=> 3x - 10x = 5 + 6 + 10
<=> -7x = 21
<=> x = -3
b. 3x + 2=8 -2(x-7)
<=> 3x + 2 = 8 - 2x + 14
<=> 3x + 2x = 8 + 14 - 2
<=> 5x = 20
<=> x = 4
c. 2x-(2+5x)= 4(x + 3)
<=> 2x - 2 - 5x = 4x + 12
<=> 2x - 5x - 4x = 12 + 2
<=> -7x = 14
<=> x = -2
d. 5-(x +8)=3x + 3(x-9)
<=> 5 - x - 8 = 3x + 3x - 27
<=> -x - 3x - 3x = -27 + 8 - 5
<=> -7x = -24
<=> x = 24/7
e. 3x - 18 + x= 12-(5x + 3)
<=> 3x - 18 + x = 12 - 5x - 3
<=> 3x + x - 5x = 12 - 3 + 18
<=> -x = 27
<=> x = - 27
a. 3(x-2)-10=5(2x + 1)
<=> 3x - 6 - 10 = 10x + 5
<=> 3x - 10x = 5 + 6 + 10
<=> -7x = 21
<=> x = -3
b. 3x + 2=8 -2(x-7)
<=> 3x + 2 = 8 - 2x + 14
<=> 3x + 2x = 8 + 14 - 2
<=> 5x = 20
<=> x = 4
c. 2x-(2+5x)= 4(x + 3)
<=> 2x - 2 - 5x = 4x + 12
<=> 2x - 5x - 4x = 12 + 2
<=> -7x = 14
<=> x = -2
d. 5-(x +8)=3x + 3(x-9)
<=> 5 - x - 8 = 3x + 3x - 27
<=> -x - 3x - 3x = -27 + 8 - 5
<=> -7x = -24
<=> x = 24/7
e. 3x - 18 + x= 12-(5x + 3)
<=> 3x - 18 + x = 12 - 5x - 3
<=> 3x + x - 5x = 12 - 3 + 18
<=> -x = 27
<=> x = - 27

Câu 1 :
a, \(\frac{3\left(2x+1\right)}{4}-\frac{5x+3}{6}=\frac{2x-1}{3}-\frac{3-x}{4}\)
\(\Leftrightarrow\frac{6x+3}{4}+\frac{3-x}{4}=\frac{2x-1}{3}+\frac{5x+3}{6}\)
\(\Leftrightarrow\frac{5x+6}{4}=\frac{9x+1}{6}\Leftrightarrow\frac{30x+36}{24}=\frac{36x+4}{24}\)
Khử mẫu : \(30x+36=36x+4\Leftrightarrow-6x=-32\Leftrightarrow x=\frac{32}{6}=\frac{16}{3}\)
tương tự
\(\frac{19}{4}-\frac{2\left(3x-5\right)}{5}=\frac{3-2x}{10}-\frac{3x-1}{4}\)
\(< =>\frac{19.5}{20}-\frac{8\left(3x-5\right)}{20}=\frac{2\left(3-2x\right)}{20}-\frac{5\left(3x-1\right)}{20}\)
\(< =>95-24x+40=6-4x-15x+5\)
\(< =>-24x+135=-19x+11\)
\(< =>5x=135-11=124\)
\(< =>x=\frac{124}{5}\)

a: =>3,6-1,7x=2,3-1,4-4=0,9-4=-3,1
=>1,7x=6,7
hay x=67/17
b: \(\Leftrightarrow30\left(5x+4\right)-15\left(3x+5\right)=24\left(4x+9\right)-40\left(x-9\right)\)
=>150x+120-45x-75=96x+216-40x+360
=>105x+45=56x+576
=>49x=531
hay x=531/49

a) \(ĐKXĐ:\hept{\begin{cases}x\ne0\\x\ne2\end{cases}}\)
\(\frac{x+2}{x-2}-\frac{5}{x}=\frac{8}{x^2-2x}\)
\(\Leftrightarrow\frac{x+2}{x-2}-\frac{5}{x}-\frac{8}{x\left(x-2\right)}=0\)
\(\Leftrightarrow\frac{x\left(x+2\right)-5\left(x-2\right)-8}{x\left(x-2\right)}=0\)
\(\Leftrightarrow x^2+2x-5x+10-8=0\)
\(\Leftrightarrow x^2-3x+2=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\x-2=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\left(tm\right)\\x=2\left(ktm\right)\end{cases}}\)
Vậy tập nghiệm của phương trình là \(S=\left\{1\right\}\)
b) Bạn viết lại chứ mik k hiểu :33

\(\left(x+4\right)\left(x^2-4x+16\right)-x\left(x-4\right)^2=8\left(x-3\right)\left(x+3\right)\)3)
\(\Leftrightarrow x^3+4^3-x\left(x-4\right)^2=8\left(x^2-3^2\right)\)
\(\Leftrightarrow x^3+64-x\left(x^2-8x+16\right)=8x^2-72\)
\(\Leftrightarrow x^3+64-x^3+8x^2-16x-8x^2-72=0\)
\(\Leftrightarrow-16x-8=0\)
\(\Leftrightarrow-8\left(2x-1\right)=0 \)
\(\Rightarrow2x-1=0\)
\(\Leftrightarrow2x=1\)
\(\Leftrightarrow x=\frac{1}{2}\)
Vậy \(x=\frac{1}{2}\)

1. Ta có :\(\left|x-7\right|=x-7\)
\(\Leftrightarrow\) \(x-7\) ∈\(\left\{\left(x-7\right);-\left(x-7\right)\right\}\)
+) Nếu \(x-7=x-7\Leftrightarrow\)\(0x=0\)(Luôn đúng ∀x)
+) Nếu \(x-7=-\left(x-7\right)\Leftrightarrow\) \(x-7=7-x\)
\(\Leftrightarrow\) 2\(x\)\(=14\)
\(\Leftrightarrow\) \(x=7\)(thỏa mãn)
Vậy phương trình có vô số nghiệm
Điều kiện xác định: x ≠ 2/7.
Suy ra: 10 – 4x = 0 ⇔ x = 5/2 (thỏa mãn đkxđ).
Vậy phương trình có tập nghiệm là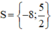
1029wieru56473892211984275678