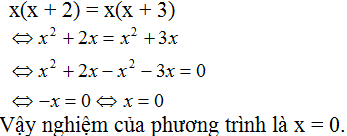K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AD
0
12 tháng 7 2017
Lời giải của bạn Hòa như trên là sai. Vì bạn đã chia cả hai vế của phương trinh cho x mà chưa biết là x = 0 hay \(x\ne0\)
Nếu \(x\ne0\)thì lời giải như trên là chính xác.
Nếu x = 0 thì phương trình có một nghiệm là 0.
18 tháng 7 2017
Nguyễn Việt Hoàng
Bạn Hòa giải sai. Vì không thể chia hai vế của phương trình đã cho với x (bởi vì x có thể = 0) để được phương trình x + 2 = x + 3. Làm như thế này có thể làm mất nghiệm của phương trình ban đầu.
- Lời giải đúng:
(Hoặc: x(x + 2) = x(x + 3)
⇔ x(x + 2) - x(x + 3) = 0 (chuyển vế)
⇔ x(x + 2 - x - 3) = 0 (rút nhân tử chung x)
⇔ x.(-1) = 0
⇔ x = 0)
TT
28 tháng 2 2020
Ta có vế trái của pt luôn \(\ge0\)
Do đó : \(11x\ge0\Rightarrow x\ge0\)
\(\Rightarrow\hept{\begin{cases}\left|x+\frac{1}{2}\right|=x+\frac{1}{2}\\...\\\left|x+\frac{1}{110}\right|=x+\frac{1}{110}\end{cases}}\)
Khi đó pt trở thành :
\(x+\frac{1}{2}+x+\frac{1}{6}+...+x+\frac{1}{110}=11x\)
\(\Leftrightarrow10x+\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{10.11}=11x\)
\(\Leftrightarrow x=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{10}-\frac{1}{11}\)
\(\Leftrightarrow x=1-\frac{1}{11}=\frac{10}{11}\) ( thỏa mãn )
Vậy : pt đã cho có nghiệm \(S=\left\{\frac{10}{11}\right\}\)
KN
28 tháng 2 2020
Dễ thấy \(VT>0\forall x\)
\(\Rightarrow11x>0\Rightarrow x>0\)
Phương trình trở thành \(10x+\left(\frac{1}{1.2}+\frac{1}{2.3}+...+\frac{1}{10.11}\right)=11x\)
\(\Rightarrow x=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{10}-\frac{1}{11}\)
\(\Rightarrow x=1-\frac{1}{11}=\frac{10}{11}\)
Vậy \(x=\frac{10}{11}\)
9 tháng 2 2017
\(\left(\frac{x+11}{115}+1\right)+\left(\frac{x+22}{104}+1\right)=\left(\frac{x+33}{93}+1\right)+\left(\frac{x+44}{82}\right)\)
<=> \(\frac{x+126}{115}+\frac{x+126}{104}=\frac{x+126}{93}+\frac{x+126}{82}\)
<=> \(\left(x+126\right)\left(\frac{1}{115}+\frac{1}{104}-\frac{1}{93}-\frac{1}{82}\right)=0\)
<=> x+126=0
<=>x=-126
3 tháng 3 2017
\(\frac{x+1006}{1007}+\frac{x+1005}{1008}=\frac{x+1004}{1009}+\frac{x+1003}{1010}\)
\(\Rightarrow\left(\frac{x+1006}{1007}+1\right)+\left(\frac{x+1005}{1008}+1\right)=\left(\frac{x+1004}{1009}+1\right)+\left(\frac{x+1003}{1010}+1\right)\)
\(\Rightarrow\frac{x+2013}{1007}+\frac{x+2013}{1008}=\frac{x+2013}{1009}+\frac{x+2013}{1010}\)
\(\Rightarrow\frac{x+2013}{1007}+\frac{x+2013}{1008}-\frac{x+2013}{1009}-\frac{x+2013}{1010}=0\)
\(\Rightarrow\left(x+2013\right)\left(\frac{1}{1007}+\frac{1}{1008}-\frac{1}{1009}-\frac{1}{1010}\right)=0\)
Mà \(\frac{1}{1007}+\frac{1}{1008}-\frac{1}{1009}-\frac{1}{1010}\ne0\)
\(\Rightarrow x+2013=0\)
\(\Rightarrow x=-2013\)
Vậy x = -2013
CM
13 tháng 3 2019
Ta có:
⇔ 15x - 3 + 10x + 15 = 2x - 16 - x
⇔ 25x - 2x + x = - 16 - 15 + 3
⇔ 24x = - 28 ⇔ x = - 7/6.
Vậy phương trình đã cho có tập nghiệm là S = { - 7/6 }.
Chọn đáp án C.
26 tháng 2 2020
\(3x^2+50x-800=0\Leftrightarrow3\left(x^2+\frac{50}{3}x-\frac{800}{3}\right)=0\)
\(\Leftrightarrow3\left(x^2-10x+\frac{80}{3}x-\frac{800}{3}\right)=0\Leftrightarrow3\left(x-10\right)\left(x+\frac{80}{3}\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=10\\x=-\frac{80}{3}\end{cases}}\).Vậy \(S=\left\{10,-\frac{80}{3}\right\}\)
26 tháng 2 2020
Nhẩm thấy có nghiệm x=10
Phân tích VT thành nhân tử: \(3x^2+50x-800=\left(3x+80\right)\left(x-10\right)\)=0
\(\Leftrightarrow\orbr{\begin{cases}3x+80=0\\x-10=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{-80}{3}\\x=10\end{cases}}}\)
Vậy phương trình có hai nghiệm như trên.
NM
Nguyễn Minh Quang
Giáo viên
5 tháng 3 2022
ta có :
\(\left|x+1\right|+\left|x-1\right|=1+\left|\left(x-1\right)\left(x+1\right)\right|\)
\(\Leftrightarrow\left|x-1\right|\left|x+1\right|-\left|x-1\right|-\left|x+1\right|+1=0\)
\(\Leftrightarrow\left(\left|x-1\right|-1\right)\left(\left|x+1\right|-1\right)=0\Leftrightarrow\orbr{\begin{cases}\left|x-1\right|=1\\\left|x+1\right|=1\end{cases}}\)
\(\Leftrightarrow x\in\left\{-2,0,2\right\}\)