Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(\frac{\pi}{2}< x< \pi\\ \Rightarrow cosx< 0,sinx>0,cotx< 0\)
\(cotx=\frac{1}{tanx}=\frac{-1}{3}\)
\(1+tan^2x=\frac{1}{cos^2x}\\ \Rightarrow cosx=\sqrt{\frac{1}{1+tan^2}}=\sqrt{\frac{1}{1+9}}=-\frac{\sqrt{10}}{10}\)
\(sinx=\sqrt{1-cos^2x}=\sqrt{1-\frac{10}{100}}=\frac{3\sqrt{10}}{10}\)

ĐKXĐ: x>=-1/2
\(\sqrt[3]{x-3}+3\sqrt{2x+1}=10\)
=>\(\sqrt[3]{x-3}-1+3\sqrt{2x+1}-9=0\)
=>\(\dfrac{x-3-1}{\sqrt[3]{\left(x-3\right)^2}+\sqrt[3]{x-3}+1}+3\left(\sqrt{2x+1}-3\right)=0\)
=>\(\dfrac{x-4}{\sqrt[3]{\left(x-3\right)^2}+\sqrt[3]{x-3}+1}+3\cdot\dfrac{2x+1-9}{\sqrt{2x+1}+3}=0\)
=>\(\left(x-4\right)\left(\dfrac{1}{\sqrt[3]{\left(x-3\right)^2}+\sqrt[3]{x-3}+1}+\dfrac{6}{\sqrt{2x+1}+3}\right)=0\)
=>x-4=0
=>x=4(nhận)

\(C=180^0-\left(A+B\right)=75^0\)
Áp dụng định lý hàm sin:
\(\dfrac{b}{sinB}=\dfrac{c}{sinC}\Rightarrow c=\dfrac{b.sinC}{sinB}=\dfrac{8.sin75^0}{sin45^0}=4+4\sqrt{3}\)

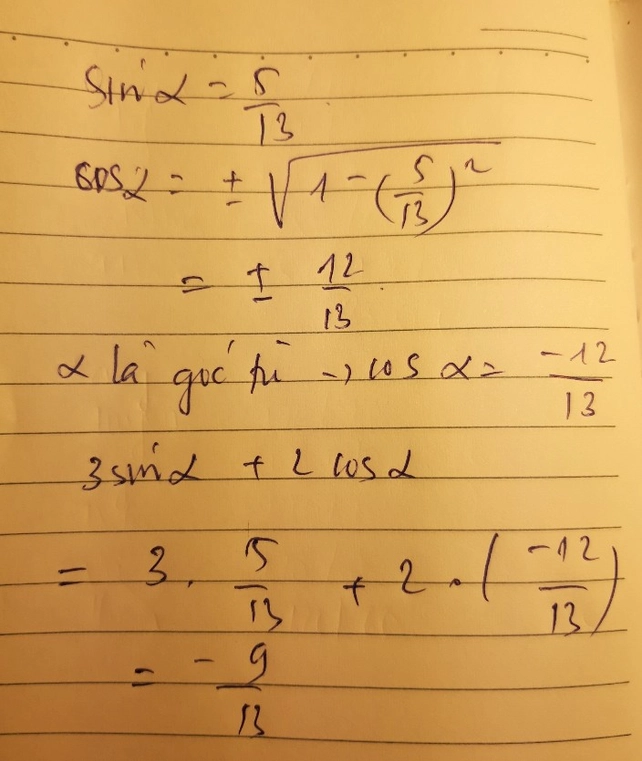


\(tan\alpha=3\)
\(1+tan^2\alpha=\dfrac{1}{cos^2\alpha}\)
\(\Rightarrow cos\alpha=\pm\sqrt{\dfrac{1}{1+tan^2\alpha}}=\pm\sqrt{\dfrac{1}{1+3^2}}=\pm\dfrac{\sqrt{10}}{10}\)
\(\Rightarrow A\)
`tan a =3 <=> (sina)/(cosa) =3 <=> sina=3cosa`
Có: `sin^2a+cos^2a =1`
`<=> (3cosa)^2 + cos^2a =1`
`<=> 10cos^2a =1`
`<=> cosa = \pm \sqrt10/10`
`=>` A.