
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 5 hình 1: (tự vẽ hình nhé bạn)
a) Xét ΔABD và ΔACB ta có:
\(\widehat{BAD}\)= \(\widehat{BAC}\) (góc chung)
\(\widehat{ABD}\)= \(\widehat{ACB}\) (gt)
=> ΔABD ~ ΔACB (g-g)
=> \(\dfrac{AB}{AC}\) = \(\dfrac{BD}{CB}\) = \(\dfrac{AD}{AB}\) (tsđd)
b) Ta có: \(\dfrac{AB}{AC}\) = \(\dfrac{AD}{AB}\) (cm a)
=> \(AB^2\) = AD.AC
=> \(2^2\) = AD.4
=> AD = 1 (cm)
Ta có: AC = AD + DC (D thuộc AC)
=> 4 = 1 + DC
=> DC = 3 (cm)
c) Xét ΔABH và ΔADE ta có:
\(\widehat{AHB}\) = \(\widehat{AED}\) (=\(90^0\))
\(\widehat{ADB}\) = \(\widehat{ABH}\) (ΔABD ~ ΔACB)
=> ΔABH ~ ΔADE
=> \(\dfrac{AB}{AD}\) = \(\dfrac{AH}{AE}\) = \(\dfrac{BH}{DE}\) (tsdd)
Ta có: \(\dfrac{S_{ABH}}{S_{ADE}}\) = \(\left(\dfrac{AB}{AD}\right)^2\)= \(\left(\dfrac{2}{1}\right)^2\)= 4
=> đpcm
Tiếp bài 5 hình 2 (tự vẽ hình)
a) Xét ΔABC vuông tại A ta có:
\(BC^2\) = \(AB^2\) + \(AC^2\)
\(BC^2\) = \(21^2\) + \(28^2\)
BC = 35 (cm)
b) Xét ΔABC và ΔHBA ta có:
\(\widehat{BAC}\) = \(\widehat{AHB}\) ( =\(90^0\))
\(\widehat{ABC}\) = \(\widehat{ABH}\) (góc chung)
=> ΔABC ~ ΔHBA (g-g)
=> \(\dfrac{AB}{BH}\) = \(\dfrac{BC}{AB}\) (tsdd)
=> \(AB^2\) = BH.BC
=> \(21^2\) = 35.BH
=> BH = 12,6 (cm)
c) Xét ΔABC ta có:
BD là đường p/g (gt)
=> \(\dfrac{AD}{DC}\) = \(\dfrac{AB}{BC}\) (t/c đường p/g)
Xét ΔABH ta có:
BE là đường p/g (gt)
=> \(\dfrac{HE}{AE}\) = \(\dfrac{BH}{AB}\) (t/c đường p/g)
Mà: \(\dfrac{AB}{BC}\) = \(\dfrac{BH}{AB}\) (cm b)
=> đpcm
d) Ta có: \(\left\{{}\begin{matrix}\widehat{HBE}+\widehat{BEH}=90^0\\\widehat{ABD}+\widehat{ADB=90^0}\\\widehat{HBE}=\widehat{ABD}\end{matrix}\right.\)
=> \(\widehat{BEH}=\widehat{ADB}\)
Mà \(\widehat{BEH}=\widehat{AED}\) (2 góc dd)
Nên \(\widehat{ADB}=\widehat{AED}\)
=> đpcm

16)
a) Tam giác ABC vuông tại A : \(AB^2+AC^2=BC^2\)
BC=10 ⇒FC=10-5.2=4.8
b) Tam giác ABC và tam giác FEC có
C chung
\(\dfrac{AC}{FC}=\dfrac{BC}{EC}=0.6\)
Do đó tam giác ABC đồng dạng với tam giác FEC (C-G-C)
c)⇒Góc FEC=ABC=AEM
Tam giác MAE và tam giác MFB có
Góc M chung
Góc AEM = MBF (CMT)
⇒ 2 Tam giác đồng dạng (G-G)
⇒\(\dfrac{MA}{MF}=\dfrac{ME}{MB}\)⇒ MA.MB=MF.MB
a) Xét \(\Delta ABC\) vuông tại A có :
\(AB^2+AC^2=BC^2\) (Định lí Py-ta-go)
=> \(BC^2=6^2+8^2=100\)
=> BC = 10 (cm)
=> CF = BC\(-\)BF = 10 - 5,2 = 4,8 (cm)
Vậy BC = 10 cm ; CF = 4,8 cm
b) Xét \(\Delta CAB\) và \(\Delta CFE\) có
\(\left\{{}\begin{matrix}\widehat{C}:chung\\\dfrac{CF}{CE}=\dfrac{CA}{CB}\left(\dfrac{4,8}{6}=\dfrac{8}{10}=\dfrac{4}{5}\right)\end{matrix}\right.\)
=>\(\Delta CAB\sim\Delta CFE\) (c-g-c)
Vậy \(\Delta CAB\sim\Delta CFE\)
c) Xét \(\Delta MAEvà\Delta MFB\) có
\(\left\{{}\begin{matrix}\widehat{M}:chung\\\widehat{MAE}=\widehat{MFB}=90^0\end{matrix}\right.\)
=> \(\Delta MAE\sim\Delta MFB\) (g-g)
=> \(\dfrac{MA}{MF}=\dfrac{ME}{MB}\)
=> MA.MB = MF.ME
Vậy MA.MB = ME.MF
d) Xét \(\Delta BMF\) và \(\Delta BCA\) có
\(\left\{{}\begin{matrix}\widehat{B}:chung\\\widehat{BFM}=\widehat{BAC}=90^0\end{matrix}\right.\)
=> \(\Delta BMF\) \(\sim\)\(\Delta BCA\) (g-g)
=> \(\dfrac{MF}{AC}=\dfrac{BF}{BA}\)
=> MF = \(\dfrac{8.5,2}{6}\) = \(\dfrac{104}{15}\approx6,9\left(cm\right)\)
Vậy MF \(\approx6,9\left(cm\right)\)

Bài 1.2
1: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
2) Ta có: \(A=\dfrac{2\sqrt{x}}{\sqrt{x}+3}-\dfrac{\sqrt{x}+1}{3-\sqrt{x}}-\dfrac{3-11\sqrt{x}}{x-9}\)
\(=\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{3-11\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2x-6\sqrt{x}+x+4\sqrt{x}+3-3+11\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{3x+9\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}-3}\)


Bài 5:
a: Ta có: \(x^2-8x+17\)
\(=x^2-8x+16+1\)
\(=\left(x-4\right)^2+1>0\forall x\)
b: Ta có: \(4x^2-12x+13\)
\(=4x^2-12x+9+4\)
\(=\left(2x-3\right)^2+4>0\forall x\)
c: Ta có: \(x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\)


Câu 3:
Gọi độ dài quãng đường AB là x(km)
Thời gian xe máy đi từ A đến B là: \(\dfrac{x}{30}\left(h\right)\)
Thời gian xe máy đi từ B về A là: \(\dfrac{x}{35}\left(h\right)\)
Theo đề, ta có phương trình: \(\dfrac{x}{30}+\dfrac{x}{35}=\dfrac{13}{3}\)
\(\Leftrightarrow\dfrac{7x}{210}+\dfrac{6x}{210}=\dfrac{910}{210}\)
\(\Leftrightarrow13x=910\)
hay x=70(thỏa ĐK)
Vậy: Độ dài quãng đường AB là 70km

\(a,\Leftrightarrow3x^2+24x-x^2-2x^2-2x=2\Leftrightarrow22x=2\Leftrightarrow x=\dfrac{1}{11}\\ b,\Leftrightarrow\left[{}\begin{matrix}5-x=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=1\end{matrix}\right.\)

 giải hộ mình mấy bài này vs ạ !
giải hộ mình mấy bài này vs ạ !






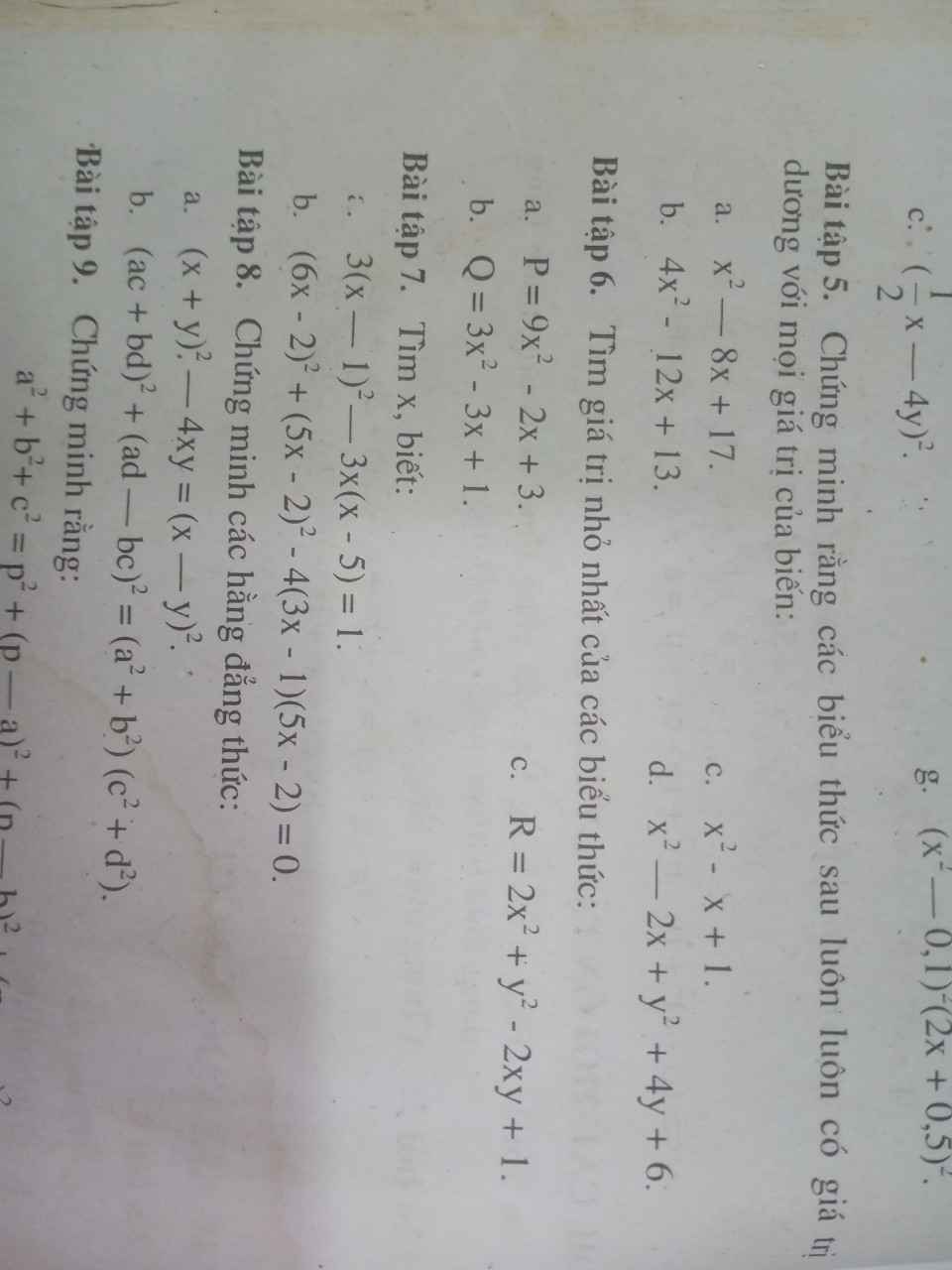



Bài 3:
Gọi giá tiền ban đầu của máy xay sinh tố là a(đồng)(Điều kiện: a>0)
Giá tiền ban đầu của bộ cốc thủy tinh là:
700000-a(đồng)
Theo đề, ta có phương trình:
\(\dfrac{9}{10}a+\dfrac{4}{5}\left(700000-a\right)=610000\)
\(\Leftrightarrow\dfrac{9}{10}a+560000-\dfrac{4}{5}a=610000\)
\(\Leftrightarrow\dfrac{1}{10}a=50000\)
hay a=500000(thỏa ĐK)
Vậy: Giá tiền ban đầu của máy xay sinh tố là 500000 đồng
Giá tiền ban đầu của bộ cốc thủy tinh là 200000 đồng
Cảm ơn nha 🥰