HD
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HD
1
26 tháng 2 2018
Trong ∆ACD ta có:
CB là đường trung tuyến kẻ từ đỉnh C
Mặt khác:
E ∈ BC và BE = 1/2 BC (gt)
Nên: CE = 2/3 CB
Suy ra: E là trọng tâm của ∆ACD.
Vì AK đi qua E nên AK là đường trung tuyến của ∆ACD
Suy ra K là trung điểm của CD
Vậy KD = KC.
E
1
16 tháng 9 2018
a. Vì |2,5 – x| = 1,3 nên 2,5 – x =1,3
=> x = 2,5 – 1,3 => x = 1,2
Hoặc 2,5 – x = -1,3 => x = 2,5 – ( -1,3)
=> x = 2,5 + 1,3 => x = 3,8
Vậy x = 1,2 hoặc x = 3,8
b. 1,6 - | x – 0,2| = 0 => |x – 0,2 | =1,6 nên x – 0,2 – 1,6
=> x = 1,6 + 0,2 => x = 1,8
Hoặc x – 0,2 = -1,6 => x= -1,6 + 0,2 => x = -1,4
Vậy x = 1,8 hoặc x = -1,4
c. |x – 1,5 | + | 2,5 – x | = 0 nên |x – 1,5| ≥ 0 ; |2,5 – x| ≥ 0
Suy ra: x – 1,5 = 0; 2,5 – x = 0 => x= 1,5 và x = 2,5
Điều này không đồng thời xảy ra. Vậy không có giá trị nào của x thoả mãn bài toán.
28 tháng 10 2017
Tổng 3 góc tam giác = 180 độ => góc FEG = 180 độ - FEG - EGF
Mà FEG và GEm bù nhau => FEG = 180 độ - GEm => EFG + EGF = GEm
10 tháng 7 2017
Vì OA là tia phân giác của xOC => xOA=AOC=12.xOCxOA=AOC=12.xOC (1)
Vì OB là tia phân giác của COy => COB=BOy=12.COyCOB=BOy=12.COy (2)
Từ (1) và (2) => xOA+BOy=AOC+BOC=12.xOC+12.COyxOA+BOy=AOC+BOC=12.xOC+12.COy
=> xOA+BOy=AOB=12.(xOC+COy)xOA+BOy=AOB=12.(xOC+COy)
=> 90o=12.xOy90o=12.xOy
=> xOy=90:12xOy=90:12
=> xOy = 90.2 = 180 => là góc bẹt
=> Ox và Oy là 2 tia đối nhau
Vậy Ox và Oy là 2 tia đối nhau
hihi
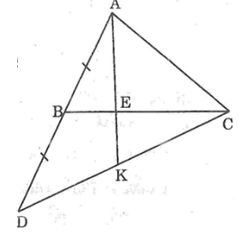
Trong ∆ACD ta có:
CB là đường trung tuyến kẻ từ đỉnh C
Mặt khác:
E ∈ BC và BE = 1/2 BC (gt)
Nên: CE = 2/3 CB
Suy ra: E là trọng tâm của ∆ACD.
Vì AK đi qua E nên AK là đường trung tuyến của ∆ACD
Suy ra K là trung điểm của CD
Vậy KD = KC.
Không vẽ hình thì thôi :)
Xét tam giác ACD ta có:
CB là đường trung tuyến
Điểm E thuộc đoạn CB và \(CE=\frac{2}{3}CB\)
Suy ra E là trọng tâm của tam giác ACD
Nên AK là đường trung tuyến của tam giác ACD
Suy ra CK = KD
Vậy CK = KD ( đpcm )
Phải mò sách lớp 7 xem lại đấy :)