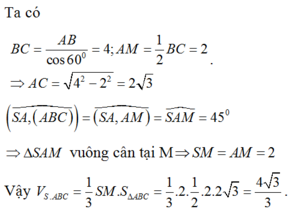Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho hình chop SABC, có đáy là ABC là tam giác vuông tại B, có độ dài các cạch AB=6,BC=8,SA=10 vuông góc với mặt đáy Tính thể tích khối chóp SABC

x s K A N B H D C
Ta có : \(\widehat{SCH}\) là góc giữa SC và mặt phẳng (ABC).
\(\Rightarrow\widehat{SCH}=60^0\)
Gọi D là trung điểm cạnh AB. Ta có :
\(HD=\frac{a}{6}\), CD= \(\frac{a\sqrt{3}}{2}\)
\(HC=\sqrt{HD^2+CD^2}=\frac{a\sqrt{7}}{3}\)
\(SH=HC.\tan60^0=\frac{a\sqrt{21}}{3}\)
\(V_{s.ABC}=\frac{1}{3}.SH.S_{\Delta ABC}=\frac{1}{3}.\frac{a\sqrt{21}}{3}.\frac{a^2\sqrt{3}}{4}=\frac{a^3\sqrt{7}}{12}\)
Kẻ Ax song song với BC, gọi N, K lần lượt là hình chiếu vuông góc của H lên Ax và SN. Ta có BC song song với mặt phẳng (SAN) và \(BA=\frac{3}{2}HA\)
Nên \(d\left(SA.BC\right)=d\left(B,\left(SAN\right)\right)=\frac{3}{2}d\left(H.\left(SAN\right)\right)\)
\(AH=\frac{2a}{3}\); \(HN=AH.\sin60^0=\frac{a\sqrt{3}}{3}\)
\(HK=\frac{SH.HN}{\sqrt{SH^2+HN^2}}=\frac{a\sqrt{42}}{12}\)
Vậy \(d\left(SA.BC\right)=\frac{a\sqrt{42}}{8}\)
Góc 60 là góc SCH. Dễ dàng tính được V
Trong (ABC), kẻ At // BC, Cz//AB, giao At=N
d(sa,bc)=d(bc, (SAN))=d(B, (SAN))=3/2 d(H, (SAN)).
Từ H kẻ HE vuông AN
Trong (SHE) kẻ HF vuông SE
=> d(H(SAN))=HF

\(SB=\sqrt{SA^2+AB^2}=2a\)
\(\dfrac{V_{SAHM}}{V_{SABC}}=\dfrac{SH}{SB}.\dfrac{SM}{SC}=\left(\dfrac{SA}{SB}\right)^2.\dfrac{SM}{SC}=\left(\dfrac{a}{2a}\right)^2.\dfrac{1}{2}=\dfrac{1}{8}\)