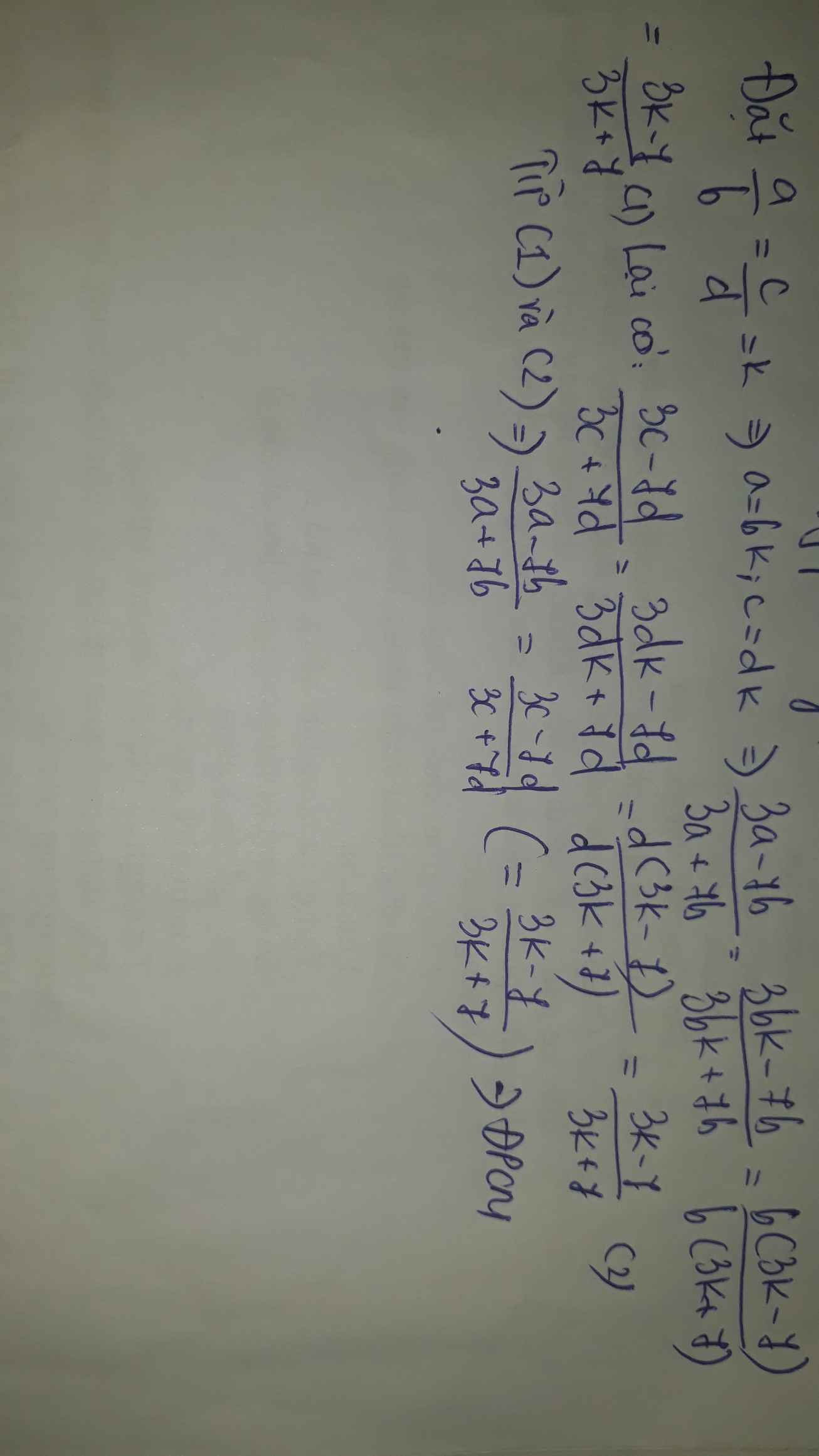
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
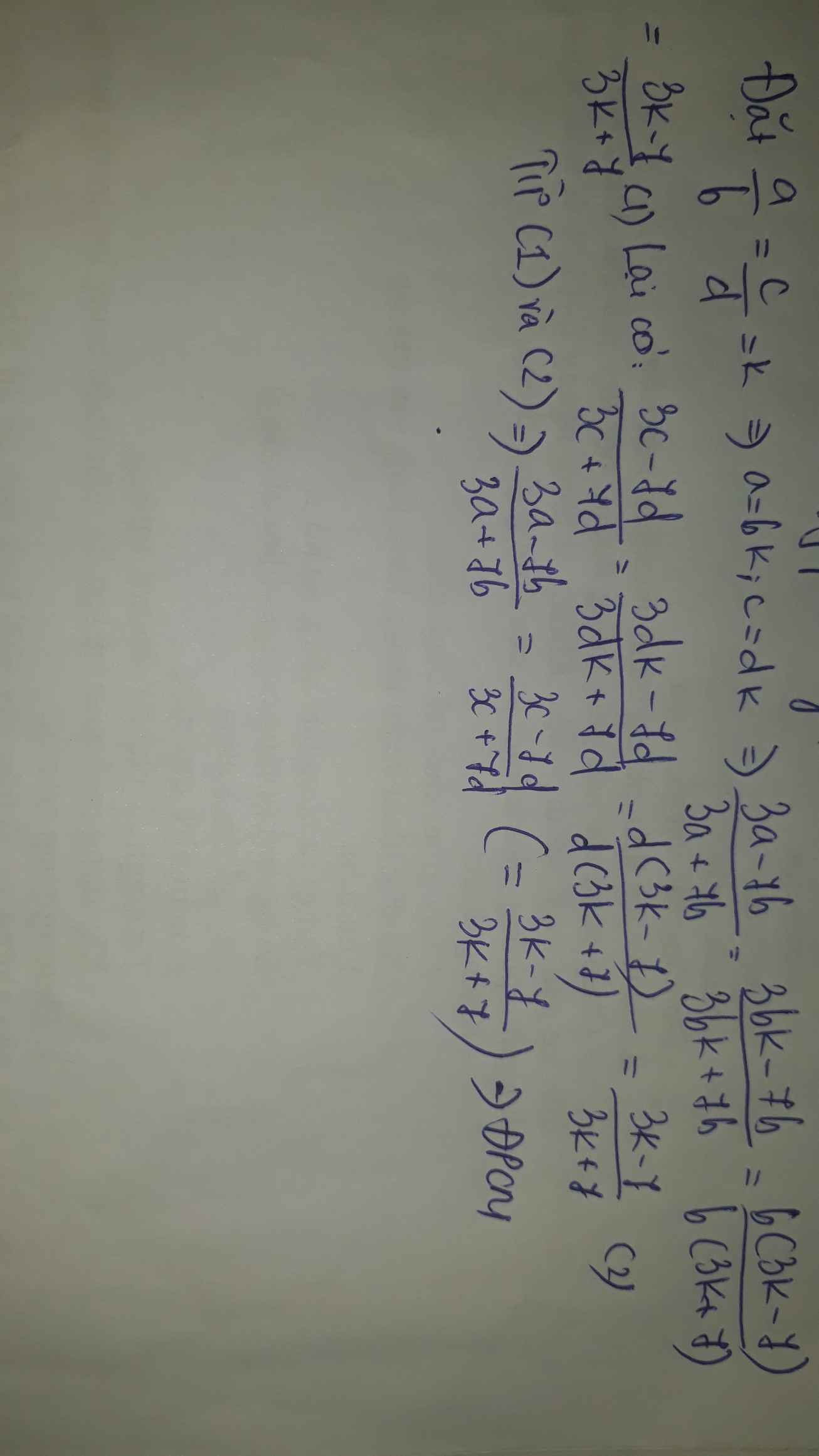
\(\dfrac{2a+13b}{3a-7b}=\dfrac{2c+13d}{3c-7d}\Rightarrow\dfrac{2a+13b}{2c+13d}=\dfrac{3a-7b}{3c-7d}\) (1)
Nhân tư và mẫu vế trái (1) với 3 và vế phải với 13 ta được:
\(\dfrac{2a+13b}{2c+13d}=\dfrac{14a+91b}{14c+91d}=\dfrac{39a-91b}{39c-91d}\)
=\(\dfrac{\left(14a+91b\right)+\left(39a-91b\right)}{\left(14c+91d\right)+\left(39c-91d\right)}=\dfrac{53a}{53c}=\dfrac{a}{c}\) (2)
Nhân tử và mẫu vế trái (1) với 3 và vế phải với 2 ta được:
\(\dfrac{2a+13b}{2c+13d}=\dfrac{6a+39b}{6c+39d}=\dfrac{6a-14b}{6c-14d}=\dfrac{53b}{53d}=\dfrac{b}{d}\) (3)
Từ (2) và (3) suy ra :
\(\dfrac{a}{c}=\dfrac{b}{d}\Rightarrow\dfrac{a}{b}=\dfrac{c}{d}\)
Ta có: \(\dfrac{2a+13b}{3a-7b}=\dfrac{2c+13d}{3c-7d}\)
\(\Rightarrow\left(2a+13b\right)\left(3c-7d\right)=\left(2c+13d\right)\left(3a-7b\right)\)
\(\Rightarrow6ac+39bc-14ad-91bd=6ac+39ad-14bc-91bd\)
\(\Rightarrow6ac-6ac+39bc+14bc-14ad-39ad-91bd+91bd=0\)
\(\Rightarrow53bc-53ad=0\)
\(\Rightarrow53bc=53ad\)
\(\Rightarrow bc=ad\)
\(\Rightarrow\dfrac{a}{b}=\dfrac{c}{d}\rightarrowđpcm.\)
\(\dfrac{2a+13b}{3a-7b}=\dfrac{2c+13d}{3c-7d}\)
\(\Leftrightarrow\)(2a+13b)(3c-7d)=(2c+13d)(3a-7b)
2a(3c-7d)+13b(3c-7d)=2c(3a-7b)+13d(3a-7b)
6ac-14ad+39bc-91bd=6ac-14bc+39ad+91bd
14ad+39bc+91bd=14bc+39ad+91bd
14ad+39bc=14bc+39ad
39bc=14bc+39ad-14ad
39bc=14bc+25ad
39bc-14bc=25ad
25bc=25ad
bc=ad
Ta có: Điều đề bài cho:
\(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow ad=bc\left(đpcm\right)\)
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\)
=>\(a=bk;c=dk\)
1: \(\dfrac{2a+3c}{2b+3d}=\dfrac{2\cdot bk+3\cdot dk}{2b+3d}=\dfrac{k\left(2b+3d\right)}{2b+3d}=k\)
\(\dfrac{2a-3c}{2b-3d}=\dfrac{2bk-3dk}{2b-3d}=\dfrac{k\left(2b-3d\right)}{2b-3d}=k\)
Do đó: \(\dfrac{2a+3c}{2b+3d}=\dfrac{2a-3c}{2b-3d}\)
2: \(\dfrac{4a-3b}{4c-3d}=\dfrac{4\cdot bk-3b}{4\cdot dk-3d}=\dfrac{b\left(4k-3\right)}{d\left(4k-3\right)}=\dfrac{b}{d}\)
\(\dfrac{4a+3b}{4c+3d}=\dfrac{4bk+3b}{4dk+3d}=\dfrac{b\left(4k+3\right)}{d\left(4k+3\right)}=\dfrac{b}{d}\)
Do đó: \(\dfrac{4a-3b}{4c-3d}=\dfrac{4a+3b}{4c+3d}\)
3: \(\dfrac{3a+5b}{3a-5b}=\dfrac{3bk+5b}{3bk-5b}=\dfrac{b\left(3k+5\right)}{b\left(3k-5\right)}=\dfrac{3k+5}{3k-5}\)
\(\dfrac{3c+5d}{3c-5d}=\dfrac{3dk+5d}{3dk-5d}=\dfrac{d\left(3k+5\right)}{d\left(3k-5\right)}=\dfrac{3k+5}{3k-5}\)
Do đó: \(\dfrac{3a+5b}{3a-5b}=\dfrac{3c+5d}{3c-5d}\)
4: \(\dfrac{3a-7b}{b}=\dfrac{3bk-7b}{b}=\dfrac{b\left(3k-7\right)}{b}=3k-7\)
\(\dfrac{3c-7d}{d}=\dfrac{3dk-7d}{d}=\dfrac{d\left(3k-7\right)}{d}=3k-7\)
Do đó: \(\dfrac{3a-7b}{b}=\dfrac{3c-7d}{d}\)
\(\dfrac{2a+13b}{3a-7b}\)=\(\dfrac{2c+13d}{3c-7d}\)
CMR:\(\dfrac{a}{b}=\dfrac{c}{d}\)
mn giải giúp cốm
Ta có: \(\dfrac{2a+13b}{3a-7b}=\dfrac{2c+13d}{3c-7d}\)
\(\Leftrightarrow\dfrac{2a+13b}{2c+13d}=\dfrac{3a-7b}{3c-7d}\)
\(\Leftrightarrow\dfrac{a}{c}+\dfrac{b}{d}=\dfrac{a}{c}-\dfrac{b}{d}\)
\(\Leftrightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
hay \(\dfrac{a}{b}=\dfrac{c}{d}\)
