Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
[Phương pháp tự luận]
Ta có : y = 6 x 2 - 6 ( m + 1 ) x + 6 m
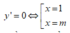
Điều kiện để hàm số có 2 điểm cực trị là m ≠ 1
![]()
Hệ số góc đt AB là k = - ( m - 1 ) 2
Đt AB vuông góc với đường thẳng y = x + 2
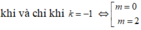

+ Ta có đạo hàm y’ = 6x2- 6( m+ 1) x+ 6m
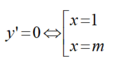
Điều kiện để hàm số có 2 điểm cực trị là : m≠ 1
Tọa độ 2 điểm cực trị là A( 1 ; 3m-1) và B ( m ; -m3+ 3m2)
+ Hệ số góc đường thẳng AB là :k= - ( m-1) 2
+ Đường thẳng AB vuông góc với đường thẳng y= x+ 2 khi và chỉ khi k= -1
Hay – ( m-1) 2= -1( vì 2 đường thẳng vuông góc với nhau thì tích hai hệ số góc bằng -1) 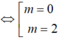
Chọn C.

1/ \(y=x^3+3x^2+mx+m-2\)
\(y'=3x^2+6x+m\)
Chia đa thức \(y\) cho \(y'\) được phần dư là \(\left(\dfrac{2m}{3}-2\right)x+\dfrac{2m}{3}-2\)
\(\Rightarrow\)Phương trình đường thẳng \(d\) đi qua 2 cực trị có dạng:
\(y=\left(\dfrac{2m}{3}-2\right)x+\dfrac{2m}{3}-2\)
Gọi A là giao điểm của \(d\) với \(Ox\Rightarrow A\left(-1;0\right)\)
Đồ thị hàm số có 2 cực trị B, C nằm về 2 phía trục hoành khi và chỉ khi A nằm giữa B và C
\(\Rightarrow x_B< -1< x_C\) với \(x_B;x_C\) là nghiệm của pt \(f\left(x\right)=3x^2+6x+m=0\)
\(\Rightarrow3.f\left(-1\right)< 0\Leftrightarrow3\left(3-6+m\right)< 0\Rightarrow m< 3\)
Vậy với \(m< 3\) thì đồ thị hs có 2 cực trị nằm về 2 phía trục hoành
2/
\(y=x^3+3mx^2+m+1\Rightarrow y'=3x^2+6mx\)
Để hàm số có 2 cực trị \(\Rightarrow m\ne0\)
Chia đa thức \(y\) cho \(y'\) được phân dư \(-2m^2x+m+1\)
\(\Rightarrow\) phương trình đường thẳng \(d\) qua 2 cực trị có dạng:
\(y=-2m^2x+m+1\)
Để \(d\) song song đường thẳng \(y=-x+2017\)
\(\Rightarrow\left\{{}\begin{matrix}-2m^2=-1\\m+1\ne2017\end{matrix}\right.\) \(\Rightarrow m=\pm\dfrac{\sqrt{2}}{2}\)

Đạo hàm y’ = 3x2+6x+m. Ta có ∆ ' y ' = 9 - 3 m
Hàm số có cực đại và cực tiểu khi ∆ ' y ' = 9 - 3 m > 0 ⇔ m < 3
Ta có 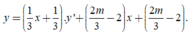
Gọi x1; x2 là hoành độ của hai điểm cực trị khi đó
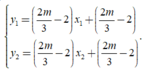
Theo định lí Viet, ta có 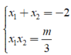
Hai điểm cực trị nằm về hai phía trục hoành khi y1.y2<0
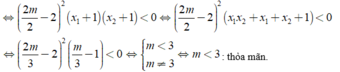
Chọn C.

1.
Đồ thị hàm bậc 3 có 2 điểm cực trị nằm về 2 phía trục hoành khi và chỉ khi \(f\left(x\right)=0\) có 3 nghiệm phân biệt
\(\Leftrightarrow x^3+3x^2+mx+m-2=0\) có 3 nghiệm pb
\(\Leftrightarrow x^3+3x^2-2+m\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x-2\right)+m\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2x+m-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2+2x+m-2=0\left(1\right)\end{matrix}\right.\)
Bài toán thỏa mãn khi (1) có 2 nghiệm pb khác -1
\(\Leftrightarrow\left\{{}\begin{matrix}1-2+m-2\ne0\\\Delta'=1-\left(m-2\right)>0\end{matrix}\right.\)
\(\Leftrightarrow m< 3\)
2.
Pt hoành độ giao điểm:
\(\dfrac{2x-2}{x+1}=2x+m\)
\(\Rightarrow2x-2=\left(2x+m\right)\left(x+1\right)\)
\(\Leftrightarrow2x^2+mx+m+2=0\) (1)
d cắt (C) tại 2 điểm pb \(\Rightarrow\) (1) có 2 nghiệm pb
\(\Rightarrow\Delta=m^2-8\left(m+2\right)>0\Rightarrow\left[{}\begin{matrix}m>4+4\sqrt{2}\\m< 4-4\sqrt{2}\end{matrix}\right.\)
Khi đó, theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=-\dfrac{m}{2}\\x_Ax_B=\dfrac{m+2}{2}\end{matrix}\right.\)
\(y_A=2x_A+m\) ; \(y_B=2x_B+m\)
\(\Rightarrow AB^2=\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2=5\)
\(\Leftrightarrow\left(x_A-x_B\right)^2+\left(2x_A-2x_B\right)^2=5\)
\(\Leftrightarrow\left(x_A-x_B\right)^2=1\)
\(\Leftrightarrow\left(x_A+x_B\right)^2-4x_Ax_B=1\)
\(\Leftrightarrow\left(-\dfrac{m}{2}\right)^2-4\left(\dfrac{m+2}{2}\right)=1\)
\(\Leftrightarrow m^2-8m-20=0\Rightarrow\left[{}\begin{matrix}m=10\\m=-2\end{matrix}\right.\)

Ta có : \(y'=3x^2+3m\)
Điều kiện để hàm số có 2 điểm cực trị là y'=0 có 2 nghiệm phân biệt
\(\Leftrightarrow 3x^2=-3m\) có 2 nghiệm phân biệt
\(\Leftrightarrow m<0\)
Đường thẳng đi qua 2 điểm cực trị là phần dư khi lấy y chia cho y':
\(x^3+3mx+1=\dfrac{x}{3}.(3x^2+3m)+2mx+1\)
\(=>\) đường thẳng đi qua 2 điểm cực trị có dạng: \(y=2mx+1\)
\(\Leftrightarrow 2mx-y+1=0\) \((\Delta)\)
\(d_{(M,\Delta)}=\dfrac{|0.2m+3.(-1)+1|}{\sqrt{4m^2+1}}=\dfrac{2}{\sqrt{5}}\)
\(\Leftrightarrow 4m^2+1=5 \Leftrightarrow m^2=1 \Leftrightarrow m=\pm1\)
Đối chiếu với điều kiện ta được \(m=1\)

Câu 2:
Tham khảo: