K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PK
5
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
1.
\(\Leftrightarrow\sqrt{2}sin\left(x-\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow sin\left(x-\dfrac{\pi}{4}\right)=0\)
\(\Leftrightarrow x-\dfrac{\pi}{4}=k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+k\pi\)
2.
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
3.
\(\Leftrightarrow\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x=\dfrac{5}{8}\)
\(\Leftrightarrow1-\dfrac{1}{2}sin^22x=\dfrac{5}{8}\)
\(\Leftrightarrow1-\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{2}cos4x\right)=\dfrac{5}{8}\)
\(\Leftrightarrow\dfrac{3}{4}+\dfrac{1}{4}cos4x=\dfrac{5}{8}\)
\(\Leftrightarrow cos4x=-\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}4x=\dfrac{2\pi}{3}+k2\pi\\4x=-\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+\dfrac{k\pi}{2}\\x=-\dfrac{\pi}{6}+\dfrac{k\pi}{2}\end{matrix}\right.\)
20 tháng 12 2021
Trong mp (ABCD), nối AN kéo dài cắt BC kéo dài tại E
⇒E∈(SBC)⇒E∈(SBC)
Do AD song song BE, áp dụng Talet:
ANNE=NDNC=1⇒AN=NE⇒ANNE=NDNC=1⇒AN=NE⇒ N là trung điểm AE
⇒MN⇒MN là đường trung bình tam giác SAE
⇒MN//SE⇒MN//(SBC)
AH
Akai Haruma
Giáo viên
15 tháng 6 2021
Câu 10:
$\sin ^2x=0\Leftrightarrow \sin x=0$
$\Rightarrow x=k\pi$ với $k$ nguyên.
Trong các khoảng đã cho chỉ có khoảng ở đáp án A chứa $k\pi$ với $k$ nguyên.
AH
Akai Haruma
Giáo viên
15 tháng 6 2021
Câu 11:
PT\(\Leftrightarrow 2\sin x\cos x-\sin x-2+4\cos x=0\)
\(\Leftrightarrow 2\cos x(\sin x+2)-(\sin x+2)=0\)
\(\Leftrightarrow (2\cos x-1)(\sin x+2)=0\)
Vì $\sin x\geq -1$ nên $\sin x+2\geq 1>0$
$\Rightarrow 2\cos x-1=0$
$\Leftrightarrow \cos x=\frac{1}{2}=\cos \frac{\pi}{3}$
$\Rightarrow x=\frac{\pi}{3}+2k\pi$ hoặc $x=-\frac{\pi}{3} +2k\pi$ với $k$ nguyên.
Đáp án B.
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2021
a.
Đặt \(sinx+cosx=t\in\left[-\sqrt{2};\sqrt{2}\right]\)
\(\Rightarrow1+2sinx.cosx=t^2\Rightarrow2sinx.cosx=t^2-1\)
Phương trình trở thành:
\(3t=2\left(t^2-1\right)\)
\(\Leftrightarrow2t^2-3t-2=0\)
\(\Rightarrow\left[{}\begin{matrix}t=2>\sqrt{2}\left(loại\right)\\t=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow sinx+cosx=-\dfrac{1}{2}\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=-\dfrac{\sqrt{2}}{8}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\\x+\dfrac{\pi}{4}=\pi-arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\\x=\dfrac{3\pi}{4}-arcsin\left(-\dfrac{\sqrt{2}}{8}\right)+k2\pi\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2021
b.
ĐKXĐ: \(x\ne\dfrac{\pi}{2}+k\pi\)
\(1+\dfrac{sinx}{cosx}=2\sqrt{2}sinx\)
\(\Rightarrow sinx+cosx=2\sqrt{2}sinx.cosx\)
\(\Leftrightarrow\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=\sqrt{2}sin2x\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=sin2x\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=x+\dfrac{\pi}{4}+k2\pi\\2x=\dfrac{3\pi}{4}-x+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k2\pi\\x=\dfrac{\pi}{4}+\dfrac{k2\pi}{3}\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k2\pi}{3}\)
HP
10 tháng 9 2021
1.
a, \(sin2x-\sqrt{3}cos2x=-1\)
\(\Leftrightarrow\dfrac{1}{2}sin2x-\dfrac{\sqrt{3}}{2}cos2x=-\dfrac{1}{2}\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{3}\right)=-\dfrac{1}{2}\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{3}\right)=sin\left(-\dfrac{\pi}{6}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\dfrac{\pi}{3}=-\dfrac{\pi}{6}+k2\pi\\2x-\dfrac{\pi}{3}=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{12}+k\pi\\x=\dfrac{3\pi}{4}+k\pi\end{matrix}\right.\)
10 tháng 9 2021
Do tổng các hệ số thứ 1,2,3 là 46 nên ta có:\(C_n^0+C_n^1+C_n^2=46\)
\(\Leftrightarrow1+\dfrac{n!}{1!\left(n-1\right)!}+\dfrac{n!}{2!\left(n-2\right)!}=46\)
\(\Leftrightarrow1+n+\dfrac{\left(n-1\right)n}{2}=46\)
\(\Leftrightarrow n^2+n-90=0\)
\(\Leftrightarrow\left[{}\begin{matrix}n=9\\n=-10\left(loai\right)\end{matrix}\right.\)
Khai triển biểu thức: \(\left(x+\dfrac{1}{x}\right)^9\)
Hạng tử thứ k+1 trong biểu thức trên
\(\left(x+\dfrac{1}{x}\right)^9=C_9^{k+1}+\left(x^2\right)^{10-k}.\left(\dfrac{1}{x}\right)^{k+1}\)
đến đây mình chịu rùi hjhj b nào làm được giúp b kia với
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 7 2021
a.
\(90^0< a< 180^0\Rightarrow cosa< 0\)
\(\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{2\sqrt{2}}{3}\)
\(tana=\dfrac{sina}{cosa}=-\dfrac{\sqrt{2}}{4}\)
b.
\(0< a< 90^0\Rightarrow cosa>0\)
\(\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{4}{5}\)
\(tana=\dfrac{sina}{cosa}=\dfrac{3}{4}\)
\(cota=\dfrac{1}{tana}=\dfrac{4}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 7 2021
c.
\(A=\dfrac{\dfrac{sina}{cosa}+\dfrac{3cosa}{sina}}{\dfrac{sina}{cosa}+\dfrac{cosa}{sina}}=\dfrac{sin^2a+3cos^2a}{sin^2a+cos^2a}=1+2cos^2a=\dfrac{17}{8}\)
d.
\(A=\dfrac{\dfrac{cosa}{sina}+\dfrac{3sina}{cosa}}{\dfrac{2cosa}{sina}+\dfrac{sina}{cosa}}=\dfrac{cos^2a+3sin^2a}{2cos^2a+sin^2a}=\dfrac{cos^2a+3\left(1-cos^2a\right)}{2cos^2a+\left(1-cos^2a\right)}\)
\(=\dfrac{3-2cos^2a}{1+cos^2a}=\dfrac{19}{13}\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
Gọi \(M\left(x;y\right)\) là 1 điểm bất kì trên (E) \(\Rightarrow\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\) (1)
Gọi \(M'\left(x';y'\right)\) là ảnh của M qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow M'\in\left(E'\right)\) với (E') là ảnh của (E) qua phép tịnh tiến nói trên
\(\left\{{}\begin{matrix}x'=x+3\\y'=y-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=x'-3\\y=y'+2\end{matrix}\right.\)
Thế vào (1):
\(\dfrac{\left(x'-3\right)^2}{16}+\dfrac{\left(y'+2\right)^2}{9}=1\)
Hay pt (E') có dạng: \(\dfrac{\left(x-3\right)^2}{16}+\dfrac{\left(y+2\right)^2}{9}=1\)
TA
6 tháng 8 2021
b) `sin^2 3x=1`
`<=> (1-cos6x)/2=1`
`<=> 1-cos6x=2`
`<=> cos6x=-1`
`<=> 6x=π +k2π`
`<=>x=π/6 +k π/3 ( k \in ZZ)`
c) `tan^2 2x=3`
`<=> (1-cos4x)/(1+cos4x)=3`
`<=> 1-cos4x=3+3cos4x`
`<=>cos4x = -1/2`
`<=>4x= \pm (2π)/3 +k2π`
`<=>x = \pm π/6 + k π/2 (k \in ZZ)`
VD
2
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 3 2021
c. Do mẫu số có nghiệm kép \(x=1\Rightarrow\)để giới hạn đã cho hữu hạn
\(\Rightarrow2\sqrt{1+ax^2}-bx-1=0\) có nghiệm kép \(x=1\)
Xét pt:
\(\sqrt{4+4ax^2}-bx-1=0\Leftrightarrow\sqrt{4+4ax^2}=bx+1\)
\(\Rightarrow4+4ax^2=\left(bx+1\right)^2=b^2x^2+2bx+1\)
\(\Rightarrow\left(4a-b^2\right)x^2-2bx+3=0\) (1)
Để (1) có nghiệm kép \(x=1\Rightarrow\left\{{}\begin{matrix}\Delta'=b^2-3\left(4a-b^2\right)=0\\\dfrac{b}{4a-b^2}=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}4a-b^2=\dfrac{b^2}{3}\\4a-b^2=b\end{matrix}\right.\) \(\Rightarrow b=\dfrac{b^2}{3}\Rightarrow\left[{}\begin{matrix}b=0\left(ktm\right)\\b=3\end{matrix}\right.\) \(\Rightarrow a=3\)
\(c=\lim\limits_{x\rightarrow1}\dfrac{2\sqrt{1+3x^2}-3x-1}{x\left(x-1\right)^2}=\dfrac{3}{8}\)
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 3 2021
d.
\(\lim\limits_{x\rightarrow+\infty}\left(\dfrac{x^2+1+\left(x-2\right)\left(ax-b\right)}{x-2}\right)=\lim\limits_{x\rightarrow+\infty}\left(\dfrac{\left(a+1\right)x^2-\left(2a+b\right)x+2b+1}{x-2}\right)\)
Giới hạn đã cho hữu hạn khi và chỉ khi \(a+1=0\Rightarrow a=-1\)
Khi đó:
\(\lim\limits_{x\rightarrow+\infty}\left(\dfrac{\left(2-b\right)x+2b+1}{x-2}\right)=\lim\limits_{x\rightarrow+\infty}\left(\dfrac{2-b+\dfrac{2b+1}{x}}{1-\dfrac{2}{x}}\right)=2-b\)
\(\Rightarrow2-b=-5\Rightarrow b=7\)
\(\Rightarrow a+b=6\)
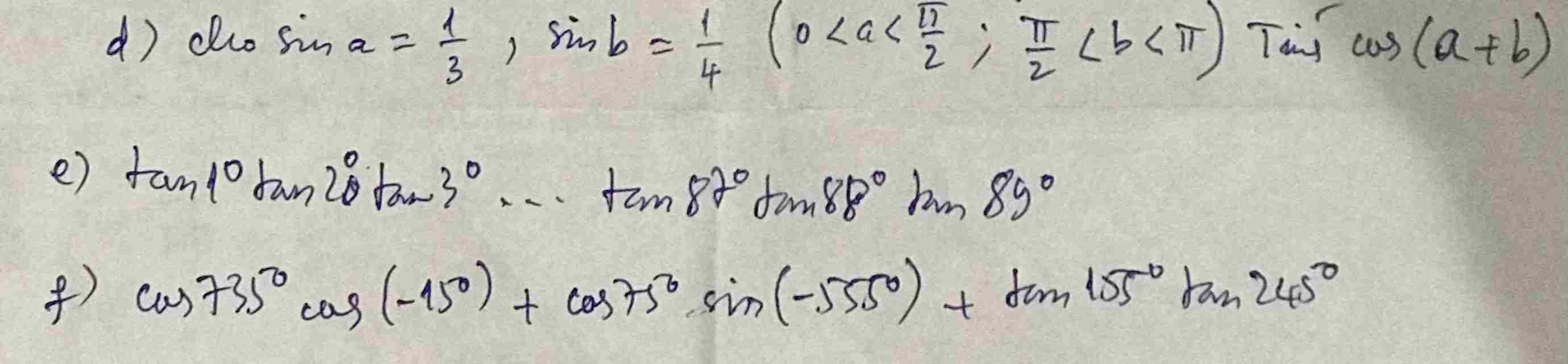
d: \(0< a< \dfrac{\Omega}{2}\) nên \(cosa>0\)
\(\dfrac{\Omega}{2}< b< \Omega\) nên cos b<0
\(sin^2a+cos^2a=1\)
=>\(cos^2a=1-\left(\dfrac{1}{3}\right)^2=\dfrac{8}{9}\)
mà cos a>0
nên \(cosa=\sqrt{\dfrac{8}{9}}=\dfrac{2\sqrt{2}}{3}\)
\(sin^2b+cos^2b=1\)
=>\(cos^2b=1-\left(\dfrac{1}{4}\right)^2=\dfrac{15}{16}\)
mà cosb<0
nên \(cosb=-\sqrt{\dfrac{15}{16}}=-\dfrac{\sqrt{15}}{4}\)
\(cos\left(a+b\right)=cosa\cdot cosb-sina\cdot sinb\)
\(=\dfrac{2\sqrt{2}}{3}\cdot\dfrac{-\sqrt{15}}{4}-\dfrac{1}{3}\cdot\dfrac{1}{4}=\dfrac{-2\sqrt{30}-1}{12}\)
e: \(tan1^0\cdot tan2^0\cdot...\cdot tan88^0\cdot tan89^0\)
\(=\left(tan1^0\cdot tan89^0\right)\cdot\left(tan2^0\cdot tan88^0\right)\cdot...\cdot\left(tan44^0\cdot tan46^0\right)\cdot tan45^0\)
\(=1\cdot1\cdot...\cdot1=1\)
f: \(cos735^0\cdot cos\left(-15^0\right)+cos75^0\cdot sin\left(-555^0\right)+tan155^0\cdot tan245^0\)
\(=cos735^0\cdot cos15^0+sin15^0\cdot sin735^0+tan155^0\cdot tan245^0\)
\(=cos\left(735-15\right)+\left(-1\right)=1-1=0\)