TN
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VQ
0
15 tháng 2 2016
Bàu 68:
-Các t/c đó đc suy ra từ các định lý:
+a,b)định lý:Tổng ba góc của một tam giác bằng 180°
+c)đl:Trong một tam giác cân,hai góc ở đáy = nhau
+d)đl:Nếu một tam giác có hai góc =nhau thì tam giác đó là tam giác cân
DM
30 tháng 12 2021
HÙGHJUJNHJRJIJKJHJUIRGJUIJUIGJUIGJUIFKJIOJUITJUIKIOUJRJUIGJUTRGJUI6JUHJUIHJYUIJUIGJUIJUIRIGIJUIERGJU6JIGJUIJUITGHJUTJUIHITGJUIYIJH
LT
0
21 tháng 11 2017
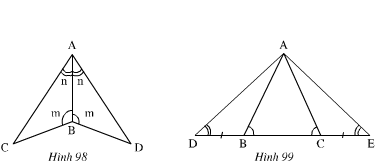
nh 98): Xét ΔABC và ΔABD có:
Nên ΔABC = ΔABD (g.c.g)
- Hình 99): Ta có:
Xét ΔABD và ΔACE có:
Nên ΔABD = ΔACE ( g.c.g)
Xét ΔADC và ΔAEB có:
DC = EB (Vì DC = DB + BC ; EB = EC + BC mà DB = EC)
Nên ΔADC = ΔAEB (g.c.g)
TH
21 tháng 11 2017
Xem hình 98)
∆ABC và ∆ABD có:
ˆA1A1^=ˆA2A2^(gt)
AB là cạnh chung.
ˆB1B1^=ˆB2B2^(gt)
Nên ∆ABC=∆ABD(g.c.g)
Xem hình 99)
Ta có:
ˆB1B1^+ˆB2B2^=1800 (Hai góc kề bù).
ˆC1C1^+ ˆC2C2^=1800 (Hai góc kề bù)
Mà ˆB2B2^=ˆC2C2^(gt)
Nên ˆB1B1^=ˆC1C1^
* ∆ABD và ∆ACE có:
ˆB1B1^=ˆC1C1^(cmt)
BD=EC(gt)
ˆDD^ = ˆEE^(gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
ˆDD^=ˆEE^(gt)
ˆC2C2^=ˆB2B2^(gt)
DC=EB
Nên ∆ADC=∆AEB(g.c.g)
NT
1
27 tháng 11 2015
bài 22
Xét ΔDAE và ΔBOC có:
AD = OB (gt)
DE = BC (gt)
AE = OC (gt)
Nên ∆DAE= ∆BOC (c.c.c)
suy ra ∠DAE = ∠BOC(hai góc tương tứng)
vậy ∠DAE = ∠xOy.
bài 23
∆BAC và ∆BAD có: AC= AD (gt)
BC = BD(gt)
AB cạnh chung.
Nên ∆BAC= ∆BAD(c.c.c)
Suy ra ∠BAC = ∠BAD (góc tương ứng)
Vậy AB là tia phân giác của góc CAD.
nhớ tick nha!!
NP
1
10 tháng 6 2016
Bài 71 :
Tam giác AHB = tam giác CKA ( c . g . c )
=> AB = CA , tam giác BHA = tam giác ACK
Ta lại có : Tam giác ACK + tam giác CAK = 90 độ
Nên tam giác BAH + tam giác CAK = 90 độ
Do đó tam giác BAC = 90 độ
Vậy tam giác ABC là tam giác vuông tại A
Bài 72
Xếp tam giác đều : Xếp tam giác với mỗi cạnh là bốn que diêm
Một tam giác cân mà ko đều : 2 cạnh bên 5 que diêm , cạnh đáy 2 que
Xét tam giác vuông : xếp tam giác có cạnh lần lượt là : ba , bốn , năm que diêm
Bài 73 ;
So sánh AC + CD vào 2 x BA
+ Xét tam giác AHB vuông tại H ,ta có :
AB2 = AH2 + HB2 ( định lý PItago )
=> HB2 =AB2 - AH2
=> HB2 = 5 - 3 = 25 - 9 =16 ( định lý Pitago )
=> HB= 4 ( vì HB > 0 )
+ Vì H nằm giữa B và C => :
HC = BC - HB = 10 - 4 = 6
+ Xét tam giác AHC vuông tại H , ta có
AC = AH + HC ( ĐỊNH LÝ PITAGO )
AC = 3 + 6 = 9 + 36 = 45
=> AC = 45 ( vì AC > 0 )
hay AC = 6,71
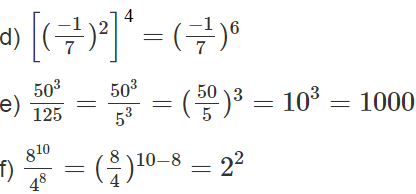
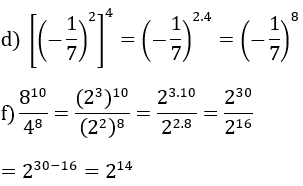
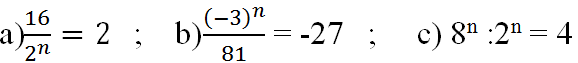
a) ∆AOD và ∆COB có:
OC =OA (gt)
OB = OD (gt)
góc xOy là góc chung
=> ∆AOD = ∆COB (cgc)
=> AD = BC
b) ∆AOD = ∆COB => góc AOD = góc BOC
=>góc BAI=gócDCI (kề bù với hai góc bằng nhau)
Vì vậy ∆DIC = ∆BIA do:
CD = AB ( OD = OB; OC = OA)
góc DCI=góc ABI ( ∆AOD = ∆COB)
góc BAI=gócDCI (chứng minh trên)
=> IC = IA và ID = IB
c) Ta có ∆OAI = ∆OIC (c.c.c)=> góc COI=gócAOI
=> OI là phân giác của góc xOy
k đi mình làm cho