Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em tham khảo:
cho 3 số x,y,z đôi một khác nhau và x+y+z=0 Tính\(P=\dfrac{2018\left(x-y\right)\left(y-z\right)\left(z-x\right)}{2xy^2+2... - Hoc24

Ta có \(x+y+z=0\)
\(\Rightarrow x+y=-z\)
\(\Leftrightarrow\left(x+y\right)^3=-z^3\)
\(\Leftrightarrow x^3+y^3+z^3+3xy\left(x+y\right)=0\)
\(\Leftrightarrow x^3+y^3+z^3-3xyz=0\)
\(\Leftrightarrow x^3+y^3+z^3=3xyz\)
Đặt \(A=2xy^2+2yz^2+2zx^2+3xyz=2xy^2+2yz^2+2zx^2+x^3+y^3+z^3\)
\(=x^2\left(2z+x\right)+y^2\left(2x+y\right)+z^2\left(2y+z\right)\)
Do \(x+y+z=0\Rightarrow\left\{{}\begin{matrix}2z+x=z-y\\2x+y=x-z\\2y+z=y-x\end{matrix}\right.\)
\(\)\(\Rightarrow A=x^2\left(z-y\right)+y^2\left(x-z\right)+z^2\left(y-x\right)\)
\(=x^2\left(z-y\right)-y^2\left(z-y+y-x\right)+z^2\left(y-x\right)\)
\(=\left(x^2-y^2\right)\left(z-y\right)-\left(z^2-y^2\right)\left(x-y\right)\)
\(=\left(x-y\right)\left(z-y\right)\left(x+y-z-y\right)\)
\(=\left(x-y\right)\left(y-z\right)\left(z-x\right)\)
\(\Rightarrow\dfrac{2018\left(x-y\right)\left(y-z\right)\left(x-z\right)}{A}=2018\)
\(\Rightarrow P=2018\)
Vậy \(P=2018\)

\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0\Leftrightarrow xy+yz+xz=0\)
\(A=\frac{yz}{x^2+yz+-xy-xz}+\frac{xz}{y^2+zx-xy-yz}+\frac{xy}{z^2+xy-xz-yz}\)
\(A=\frac{yz}{\left(x-y\right)\left(x-z\right)}+\frac{xz}{\left(y-z\right)\left(y-x\right)}+\frac{xy}{\left(z-x\right)\left(z-y\right)}\)
\(A=\frac{yz\left(y-z\right)-xz\left(x-z\right)+xy\left(x-y\right)}{\left(x-z\right)\left(x-y\right)\left(y-z\right)}\)
\(A=\frac{\left(z-x\right)\left(y-z\right)\left(y-x\right)}{\left(x-z\right)\left(x-y\right)\left(y-z\right)}=1\)

\(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\Leftrightarrow\dfrac{xy+yz+xz}{xyz}=0\Leftrightarrow xy+yz+xz=0\Leftrightarrow yz=-xy-xz\)
Ta có \(x^2+2yz=x^2+yz-xy-xz=\left(x-y\right)\left(x-z\right)\)
Tương tự \(y^2+2xz=\left(y-x\right)\left(y-z\right);z^2-2xy=\left(z-x\right)\left(z-y\right)\)
\(A=\dfrac{yz}{x^2+2yz}+\dfrac{xz}{y^2+2xz}+\dfrac{xy}{z^2+2xy}=\dfrac{yz}{\left(x-y\right)\left(x-z\right)}+\dfrac{xz}{\left(y-z\right)\left(y-x\right)}+\dfrac{xy}{\left(z-x\right)\left(z-y\right)}\\ A=\dfrac{-yz\left(y-z\right)-xz\left(z-x\right)-xy\left(x-z\right)}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}\\ A=\dfrac{-yz\left(y-z\right)+xz\left(y-z\right)+xz\left(x-y\right)-xy\left(x-y\right)}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}\\ A=\dfrac{\left(y-z\right)\left(xz-yz\right)+\left(x-y\right)\left(xz-xy\right)}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}\\ A=\dfrac{\left(x-y\right)\left(y-z\right)\left(z-x\right)}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}=1\)
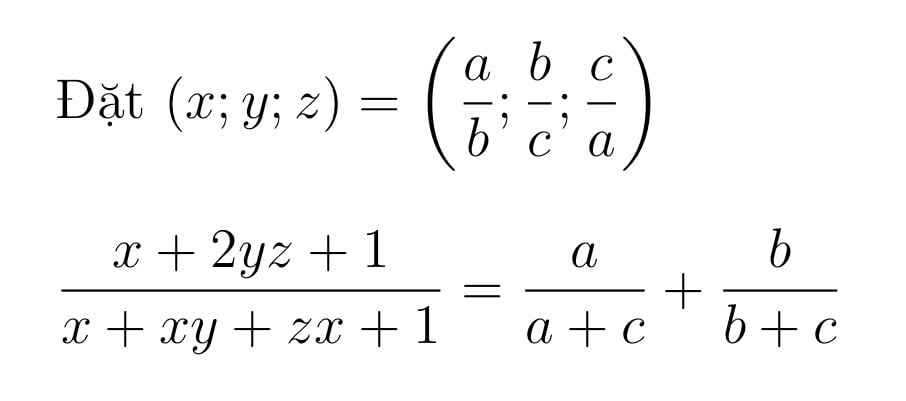
giúp ko biết đc j ko nhỉ ^^
ta có \(x+y+z=0\Rightarrow x^3+y^3+z^3=3xyz.\)lúc đó
\(P=\frac{2018\left(x-y\right)\left(y-z\right)\left(z-x\right)}{2xy^2+2yz^2+2zx^2+3xyz}=2018.\frac{xy^2+yz^2+zx^2-x^2y-y^2z-z^2x}{xy^2+yz^2+zx^2+y^2\left(x+y\right)+x^2\left(x+z\right)+z^2\left(z+y\right)}\)
\(P=2018.\frac{xy^2+yz^2+zx^2-x^2y-y^2z-z^2x}{xy^2+yz^2+zx^2-x^2y-y^2z-z^2x}=2018\)