
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



gọi x là cạnh của tam giác đều ABC
=> đg cao AH = \(\dfrac{x\sqrt{3}}{2}\) = 2a
=> \(x=\dfrac{4a\sqrt{3}}{3}\)
=>r=\(\dfrac{2a\sqrt{3}}{3}\)
Sxq = \(\pi rl\) = \(\pi.\dfrac{2a\sqrt{3}}{3}\).\(\dfrac{4a\sqrt{3}}{3}\) = \(\dfrac{8\pi}{3}\)



a) ![]() . Tập xác định : R
. Tập xác định : R  {
{![]() } ;
} ;
![]() và
và ![]() ;
;
Do đó hàm số luôn đồng biến trên mỗi khoảng xác định của nó.
b) Tiệm cận đứng ∆ : x = ![]() .
.
A(-1 ; 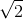 ) ∈ ∆ ⇔
) ∈ ∆ ⇔ ![]() = -1 ⇔ m = 2.
= -1 ⇔ m = 2.
c) m = 2 => 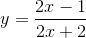 .
.
a) ![]() . Tập xác định : R
. Tập xác định : R  {
{![]() } ;
} ;
![]() và
và ![]() ;
;
Do đó hàm số luôn đồng biến trên mỗi khoảng xác định của nó.
b) Tiệm cận đứng ∆ : x = ![]() .
.
A(-1 ; 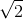 ) ∈ ∆ ⇔
) ∈ ∆ ⇔ ![]() = -1 ⇔ m = 2.
= -1 ⇔ m = 2.
c) m = 2 => 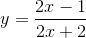 .
.
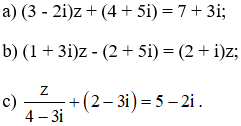
kết quả của em là 116 đúng không ạ đúng đúng không đùng thì đúng