
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.

\(sin^2x+\sqrt{3}sinxcosx=1\)
\(\Leftrightarrow sin^2x+\sqrt{3}sinxcosx=sin^2x+cos^2x\)
\(\Leftrightarrow cosx\left(\sqrt{3}sinx-cosx\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}cosx=0\\\sqrt{3}sinx=cosx\end{cases}}\Leftrightarrow\orbr{\begin{cases}cosx=0\\tanx=\frac{1}{\sqrt{3}}\end{cases}}\)
Từ đây suy ra nghiệm.

I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.

1+1+1+1+1+1+1+1+1+1+1+1+1+1+1+=???
Phép tính như thế thì mời nhà toán hok về lm giùm!
KO NÊN ĐĂNG CÂU HỎI LINH TINH!
#Biinz_Tổng's
#Dương_Hoàng_Anh

I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.

Phần I hôm qua mình trl rồi .
Phần II
Câu 1: Chỉ ra các phương thức biểu đạt chính của văn bản?
Các PTBĐ : Tự sự , miêu tả , biểu cảm .
Câu 2: Kể tên ít nhất 2 truyện cổ hoặc 2 câu ca dao được gợi nhớ trong khổ thơ 1 và 2.
- 2 truyện cổ tích được gợi nhớ trong khổ 1 & 2 :
+ Tấm cám .
+ Sự tích cây Khế.


\(\Omega=C^2_{52}.C^2_{52}\)
a) Trong mỗi bộ có 4 lá K nên số trường hợp rút được 2 K là \(C^2_4\)
\(\Rightarrow P=\frac{C_4^2.C_4^2}{C_{52}^2.C_{52}^2}=\frac{1}{48841}\)
b) Vì bích, rô , nhép, cơ mỗi bộ có 13 lá nên số trường hợp rút được 1 lá mỗi loại là: \(\left(C_{13}^1\right)^4\)
Vì mỗi bộ chỉ được rút 2 lá nên nếu bộ 1 rút được 2 nguyên tố này thì bộ 2 phải rút được 2 nguyên tố kia
---> Số trường hợp bốc được: \(C_4^2\)
\(\Rightarrow P=\frac{C_4^2.\left(C_{13}^1\right)^4}{\left(C_{52}^2\right)^2}=\frac{169}{1374}\)
c) Nếu bộ 1 bốc được 2 con Q nguyên tố này thì 2 con Q của các nguyên tố còn lại phải nằm ở bộ 2
---> Số trường hợp bốc: \(C_4^2\)
\(\Rightarrow P=\frac{C_4^2}{\left(C_{52}^2\right)^2}=\frac{1}{293046}\)

\(2tan^2x-2\sqrt{3}tanx-3=0\)
\(\orbr{\begin{cases}tanx=\frac{3+\sqrt{3}}{2}\\tanx=\frac{-3+\sqrt{3}}{2}\end{cases}}\)
\(\orbr{\begin{cases}tanx=tana\\tanx=tanb\end{cases}}\) Đặt \(tana=\frac{3+\sqrt{3}}{2};tanb=\frac{-3+\sqrt{3}}{2}\)
\(\orbr{\begin{cases}x=a+k\pi\\x=b+k\pi\end{cases};k\in Z}\)
\(\sqrt{3}cot^2x-\left(1+\sqrt{3}\right)cotx+1=0\)
\(\orbr{\begin{cases}cotx=1\\cotx=\frac{\sqrt{3}}{3}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}tanx=1=tan\frac{\pi}{4}\\tanx=\sqrt{3}=tan\frac{\pi}{3}\end{cases}}\)
\(\orbr{\begin{cases}x=\frac{\pi}{4}+k\pi\\x=\frac{\pi}{3}+k\pi\end{cases};k\in Z}\)
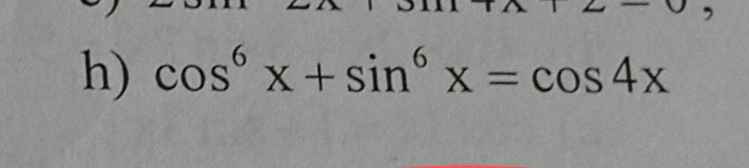 giai chi tiết giúp e với!!!
giai chi tiết giúp e với!!!
Pt \(\Leftrightarrow\left(cos^2x+sin^2x\right)^3-3cos^2x.sin^2x\left(cos^2x+sin^2x\right)=1-2sin^22x\)
\(\Leftrightarrow1-\dfrac{3}{4}sin^22x=1-2sin^22x\)
\(\Leftrightarrow\dfrac{5}{4}sin^22x=0\)\(\Leftrightarrow sin2x=0\Leftrightarrow x=\dfrac{k\pi}{2}\) \(\left(k\in Z\right)\)
Vậy...