K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LT
giúp e giải gấp với ạ mấy câu lí thuyết thì ghi đáp án thôi còn mấy câu bài toán thì giải chi tiết ạ
0
LT
0
22 tháng 7 2016
Trước tiên ta biểu diễn theo phương trình hình tròn :
Với : \(\varphi=-\frac{\pi}{2}\left(rad\right)=90^O\)
Vật xuất phát từ điểm M (vị trí cân bằng theo chiều dương)
\(\Delta t=t_2-t_1=\frac{\pi}{12}\left(s\right)\)
Góc quét : \(\Delta\varphi=\Delta t.\omega=\frac{\pi}{12}.50=\frac{25\pi}{6}\)
Phân tích góc quét : \(\Delta=\frac{25\pi}{6}=\frac{\left(24+1\right)\pi}{6}=2.2\pi+\frac{\pi}{6}\)
Vậy: \(\Delta\varphi_1=2,2\pi\) ; \(\Delta\varphi_2=\frac{\pi}{6}\)
Khi góc quét \(\Delta\varphi_1=2.2\pi\) thì s1 = 2.4.A =2.4.12 = 96 (quay vòng quanh M)
Khi góc quét : \(\Delta\varphi_2=\frac{\pi}{6}\) vật đi từ M đến N thì s2 = 12cos600
Vậy quãng đường tổng cộng : s1 + s2 = 96 + 6 = 102 (cm)
22 tháng 7 2016
Biểu diễn dao động điều hòa bằng véc tơ quay, trong thời gian \(\pi/12\)s thì véc tơ quay đã quay 1 góc là: \(\alpha=\omega .t =50.\dfrac{\pi}{12}=\dfrac{25\pi}{6}(rad)=4\pi+\dfrac{\pi}{6}\)
+ Véc tơ quay quay đc góc \(4\pi\), bằng 2 chu kì thì quãng đường là: \(S_1=2.4A=8.12=96cm\)
+ Quay thêm góc \(\pi/6\) từ VTCB thì quãng đường đi thêm được là: \(S_2=A/2=6cm\)
Vậy quãng đường vật đi được là: \(S=S_1+S_2=96+6=102cm\)
TT
giải chi tiết 3 bài này dùm em vs ạ 
0
14 tháng 8 2023
10B
x=A*cos(\(\omega t+\varphi\))
x=5*cos(\(\omega t\))
=>A=5
11A:
Biên độ dao động bằng quỹ đạo chia đôi
=>A=MN/2=15cm
12C
\(y=-10\cdot cos\left(4\Pi t-\dfrac{pi}{4}\right)=10\cdot cos\left(4\Pi t+\dfrac{pi}{4}\right)\)
=>Pha dao động ban đầu là pi/4
13C
\(y=-8cos\left(2t+\dfrac{pi}{2}\right)=8\cdot\left[-cos\left(2t+\dfrac{pi}{2}\right)\right]\)
\(=8\cdot cos\left(2t-\dfrac{pi}{2}\right)\)
=>Pha dao động ban đầu là -pi/2
KA
17 tháng 12 2023
`3 <= 16/(2k+1) <= 5`
$\bullet$ `3 <= 16/(2k+1) <=> 6k + 3 <= 16 <=> 6k <= 13`
`<=> k <= 2,16`
$\bullet$ `16/(2k +1) <= 5`
`<=> 16 <= 10k + 5`
`<=> k >= 1,1`
Từ đó suy ra: `1,1 <= k <= 2,16`.
EF
17 tháng 12 2023
Cho tam giác ABC có AB = AC và BC < AB. M là trung điểm của BC.
a. tam giác ABM = tam giác ACM, AM là tia phân giác của góc BAC.
b. Trên cạnh AB lấy điểm N sao cho CB = CD, CN là tia phân giác của góc BCD. Chứng minh: CN vuông góc với BD.
c. Trên tia đối của tia CA lấy điểm E sao cho AD = CE. Chứng minh: BE - CE = 2BN.
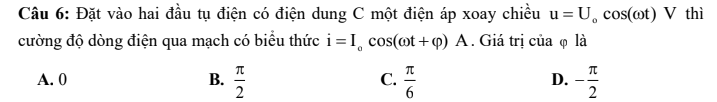
C