
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.
Trong mp (SBC), nối EM kéo dài cắt BC tại P
\(\left\{{}\begin{matrix}P\in EM\subset\left(MEF\right)\Rightarrow P\in\left(MEF\right)\\P\in BC\end{matrix}\right.\)
\(\Rightarrow P=BC\cap\left(MEF\right)\)
b.
\(\left\{{}\begin{matrix}P\in BC\subset\left(ABC\right)\\F\in AB\subset\left(ABC\right)\end{matrix}\right.\) \(\Rightarrow PF\subset\left(ABC\right)\)
Trong mp (MEF), nối MN và PF kéo dài cắt nhau tại Q
\(\left\{{}\begin{matrix}Q\in MN\\Q\in PF\subset\left(ABC\right)\Rightarrow Q\in\left(ABC\right)\end{matrix}\right.\)
\(\Rightarrow Q=MN\cap\left(ABC\right)\)
c.
Trong mp (SCF), nối CN cắt MF tại H
\(\left\{{}\begin{matrix}H\in CN\\H\in MF\subset\left(MAB\right)\end{matrix}\right.\) \(\Rightarrow H=CN\cap\left(MAB\right)\)

a.
Kéo dài AB và DC cắt nhau tại E
Trong mp (SCD), nối EM kéo dài cắt SD tại F
\(\Rightarrow\) Tứ giác ABMF là thiết diện của (BAM) và chóp
b.
Trong mp (SCD), nối MN kéo dài cắt SE tại P ( điểm E được dựng ở câu a)
Trong mp (SAB), nối AP cắt SB tại Q
\(\Rightarrow\) Tứ giác ANMQ là thiết diện của (MAN) và chóp


3)\(sin6x.sin2x=sin5x.sinx\)
\(\Leftrightarrow\dfrac{1}{2}\left(cos4x-cos8x\right)=\dfrac{1}{2}\left(cos4x-cos6x\right)\)
\(\Leftrightarrow cos8x=cos6x\)
\(\Leftrightarrow\left[{}\begin{matrix}8x=6x+k2\pi\\8x=-6x+k2\pi\end{matrix}\right.\) (\(k\in Z\)) \(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{k\pi}{7}\end{matrix}\right.\)(\(k\in Z\))
Vậy...
13)\(cosx.cos3x-sin2x.sin6x-sin4x.sin6x=0\)
\(\Leftrightarrow\dfrac{1}{2}.\left(cos2x+cos4x\right)-\dfrac{1}{2}\left(cos4x-cos8x\right)-\dfrac{1}{2}\left(cos2x-cos10x\right)=0\)
\(\Leftrightarrow cos8x+cos10x=0\)
\(\Leftrightarrow2.cos9x.cosx=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos9x=0\\cosx=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{18}+\dfrac{k\pi}{9}\\x=\dfrac{\pi}{2}+k\pi\end{matrix}\right.\) (\(k\in Z\))
Vậy...

Gọi \(\overrightarrow{v}=\left(a;b\right)\)
d nhận \(\left(4;3\right)\) là 1 vtcp, mà \(\overrightarrow{v}\) vuông góc d \(\overrightarrow{v}=\left(3k;-4k\right)\)
Chọn \(M\left(-1;0\right)\in d\) , do \(T_{\overrightarrow{v}}\left(d\right)=d_1\Rightarrow\) ảnh \(M_1\left(x_1;y_1\right)\) của \(M\) qua phép tịnh tiến \(\overrightarrow{v}\) nằm trên \(d_1\)
\(\left\{{}\begin{matrix}x_1=-1+3k\\y_1=0-4k=-4k\end{matrix}\right.\) \(\Rightarrow M_1\left(-1+3k;-4k\right)\)
Thế vào pt \(d_1\)
\(3\left(-1+3k\right)-4.\left(-4k\right)-2=0\) \(\Rightarrow k=\dfrac{1}{5}\)
\(\Rightarrow\overrightarrow{v}=\left(\dfrac{3}{5};-\dfrac{4}{5}\right)\)


Số hạng đó là số hạng thứ 4 \(\Rightarrow k=3\) nên có dạng:
\(C_6^3\left(2x\right)^3.\left(-y^2\right)^3=-C_6^3\left(2x\right)^3y^6\)

Đồng nhất hệ số 2 vế thôi, hệ số các vecto bên vế trái bằng với vế phải (bên vế trái ko có \(\overrightarrow{c}\) nên coi như hệ số của nó bằng 0, do đó \(-\left(2m+n\right)=0\Rightarrow2m+n=0\))


\(y'=\dfrac{4.3}{8}.x^3+\dfrac{5.3}{6}x^2-\dfrac{2}{2\sqrt{x}}+3=\dfrac{3x^3}{2}+\dfrac{5x^2}{2}-\dfrac{1}{\sqrt{x}}+3\)





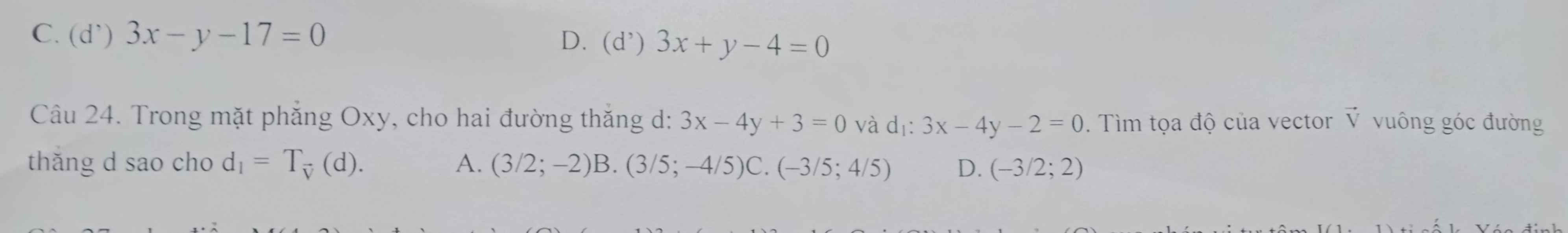


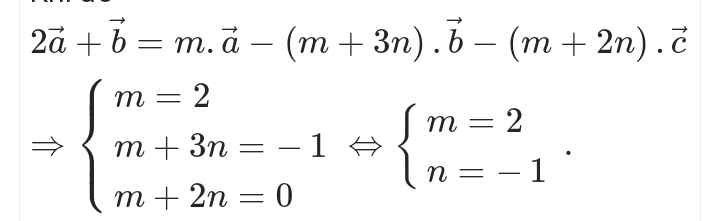

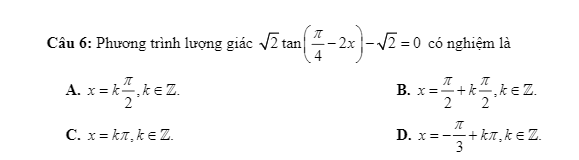
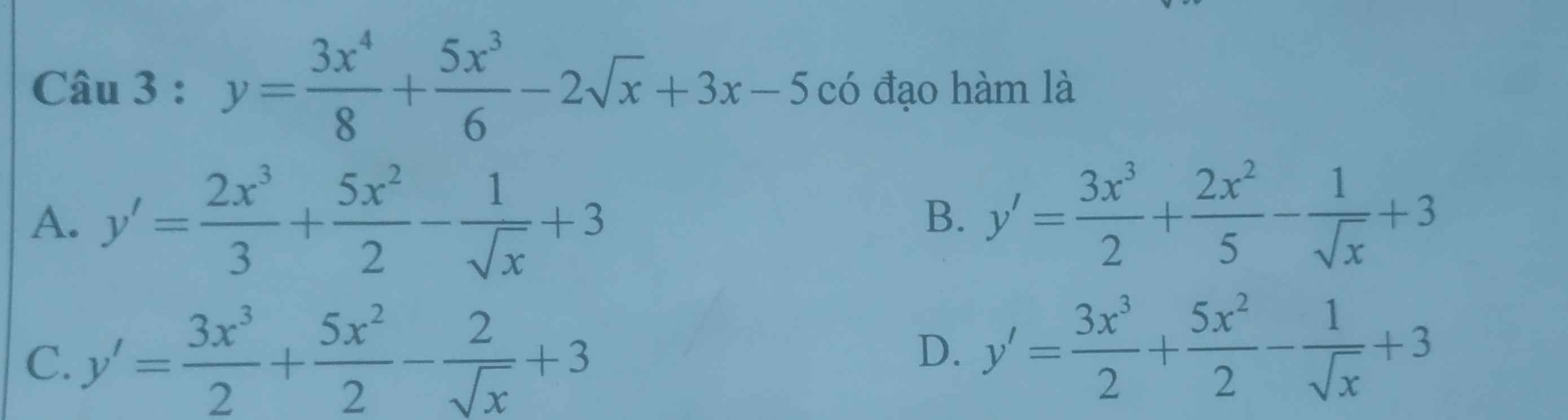 cho đáp án và giải thích giùm mình với ạ
cho đáp án và giải thích giùm mình với ạ
Đề là gì bạn?
Tìm txdd đó